The Creation of Musical Scales

from a mathematic and acoustic point of view, Part II,

by Thomas Váczy Hightower

   My first search was to look at musical practice in ancient times, not only in Europe but all over the world. There were several other musical scales besides the diatonic scale, where the semitones were located in other places than from me-fa and si-do. In the Gregorian modals, for instance, the different placement of the semitones creates the specific modes.

Pentatonic Music

In pentatonic folk music semitones do not exist. By practical experience, people have found out that the five-note scale allowed the possibility of playing in any key without significant disharmony. Theorists would say that the scale was composed of ascending and descending fifths, only in two steps in each direction. A pentatonic scale can be played by only using the black keys on the piano.

EASTERN MUSIC

After a study of ancient main cultural music, mainly Chinese and Indian, I realized how universal the concept of the octave was in every musical culture.
According to Helmholtz, the Arabic and Persian scales, and the Japanese and the Pacific scales are also within an octave. However, the division of the octave differs from culture to culture.
Arab music divides the octave into sixteen unequal intervals. The Persians divided their octave into 24 steps, so they must have used quarter tones. From excavated Egyptian flutes, a seven note scale C, D, E, F#, G, A, B, has been discovered, which is identical with the Syntolydian scale of ancient Greece. Japanese music used mainly a pentatonic scale.

Chinese music

Music was the cornerstone of the Chinese civilization, the longest living culture in history. It was considered to embody within its tones elements of the celestial order. The audible sound, including music, was but one form of manifestation of a much more fundamental form of Super-physical Sound. The fundamental Primal Sound was synonymous with that which the Hindus call OM. The Chinese believed that this Primal Sound, Kung or ‘Huang Chung’ (directly translated ‘yellow bell’) was, though inaudible, present everywhere as a Divine Vibration.
Furthermore, it was also divided into 12 lesser Sounds or Tones. These twelve Cosmic Tones were emanations of, and an aspect of, the Primal Sound, but were closer in vibration to the tangible, physical world. Each of the 12 Tones was associated with one of the 12 zodiacal regions of the heavens.

Audible sound was conceived as being a physical level manifestation of the 12 tones. Sound on Earth was a kind of sub-tone of the celestial vibration. It was believed to contain a little part of the celestial tones' divine power.
“As above, so below”, as the Egyptian Hermes Thot said. In the Lord’s Prayer, a similar wish is spoken.

For the ancient Chinese, the alignment with the divine prime tone was the Emperor's most important task. The alignment of earth with heaven, and man with the Supreme, was literally the purpose of life. The entire order and affairs of the State were dependent upon the right tuning of the fundamental tone, the ‘yellow bell’, or Kung.

As an ancient text warns: “If the Kung is disturbed, then there is disorganization; the prince is arrogant.”
If the Kung was out of tune, because the celestial realm has changed, disorder and inharmonious behavior in society became obvious. Every instrument (including measuring instruments) was tuned and utilized in accordance with the holy tone.

The instrument that could give to man the fundamental tone for a musical scale in perfect harmony with the universe was the key to earthly paradise, and essential to the security and evolution of society.
It became the Chinese Holy Grail.
One legend tells of the amazing journey of Ling Lun, a minister of the second legendary Chinese Emperor, Huang Ti. Ling Lun was sent like an ancient Knight of King Arthur to search for a special and unique set of bamboo pipes. These pipes were so perfect that they could render the precise standard pitches to which all other instruments throughout the land could be tuned. 

That sacred tone, which relates to the Western modern pitch of F, was considered as the fundamental cosmic tone. The Chinese were aware of the slow changing cosmic influence, and consequently the Kung has to change accordingly. The Emperor had the task of tuning the Kung so it was in alignment with the cosmic tone.

Tuning the Sacret Kung

Cousto has in his book The Cosmic Octave an interesting observation on this matter. He relates the Kung to the frequency of the Platonic Year. The duration of the Platonic Year, (The Pythagorean Great Year) is about 25,920 years and represents the amount of time the axis of the Earth takes to complete a full rotation. 

The vernal equinox is the point at which the equator (of Earth) intersects the ecliptic (or zodiac), which is the position of the sun at the beginning of spring - March 21st.
The vernal equinox takes an average of 2,160 years to travel through one sign of the zodiac. This period of time is known as an age. It is not possible to state exactly when one age is ending and a new beginning, because the signs overlap to a certain degree. 
The journey of the vernal equinox through each of the 12 signs of the Zodiac equals one great year of approximately 25,920 years. (Presently we are on the cusp of Aquarius as the age of Pisces is ending). 
This number of years is close to the high number of generating fifths when we come into a cycle of 25,524 notes. 

Cousto calculates the note of the Platonic year to be F in the Western Equal Temperament pitch, which is found in the 48th octave with a frequency of 344.12 Hz., or in the 47th octave to be 172.06 Hz. Note that the corresponding a' has a frequency of 433.564 Hz. (Modern Western concert pitch is 440 Hz.)
Calculation: 31 556 925.97(the tropical year in seconds) * 25,920 (Platonic year). Since the length (of a vibrating string, or the period of time) is in reverse proportionality to the frequency, the length of the Platonic year in seconds shall be the denominator. The frequency is very low, so we will raise the frequency to the range of hearing by multiplying with the necessary amount of octaves, e.g. 48 octaves so we arrive to 344,12 Hz. (47 octaves will be the half, 172,06 Hz.)
If we want to reach the spectrum of light, we multiply with 89 octaves which leads us to a frequency of 1/31 556 925.97 * 1/25 920 * 2 89 = 7,56 * 10 14 Hz. corresponding to a wavelength of 0.396 micrometer, which we perceive as violet near the ultra violet. This is the color of the Platonic Year. The complementary color to violet is yellow. Their fundamental tone was called the yellow bell.

It is a wonder for me how the ancient Chinese could be aware of their sacred fundamental tone, Kung, being in accordance with the Platonic Year, and choose the great rhythm of the Earth. 

Creation of a scale

It might be a surprise that the diatonic scale was the foundation for the ancient Chinese and the Indian music, though the musical theory and practices differ from the Western. 

For the old Chinese, their musical scale was developed by the circle of perfect fifths up to 60 degrees or keys, the 60 Lü, though they usually only used the first 5 fifths in their pentatonic music, because they knew that these represent the limit of consonance in modal music. In addition, the ancient Chinese saw a symbolic representation in the pentatonic scale, rooted in their belief in music as being the representation of the relationship between heaven and earth (the five elements). 

The Chinese were well aware centuries ago of the existence of our modern Equal Temperament. They dismissed such a tempered scale not only for its badly false notes, but mainly because the tuning was not in alignment with the cosmic tone.
According to the book by David Taime, The Secret Power of Music, 3 was the symbolic numeral of heaven and 2 that of the earth; sounds in the ratio of 3:2 will harmonize heaven and earth. As a way to apply that important concept, the Chinese took the foundation note, ‘Huang Chung’, and from it produced a second note in the ratio of 3:2.

A more in-depth explanation made by Alain Daniélou in his ”Music and the Power of Sound”:
“Music, being the representation of the relationship between heaven and earth, must quite naturally have this confirmation of a center or tonic (gong) surrounded by four notes assimilated to the four directions of space, the four perceptible elements, the four seasons, and so on. "

“The pentatonic scale thus presents a structure that allows it to be an adequate representation of the static influence of heaven on earth. But a static representation of a world in motion could not be an instrument of action upon that world. It is necessary to evolve from the motionless to the moving, from the angular to the circular, from the square to the circle. To express the movements of the universe, the sounds will have to submit to the cyclic laws that, in their own field, are represented by the cycle of fifths.”

The spiral of fifths

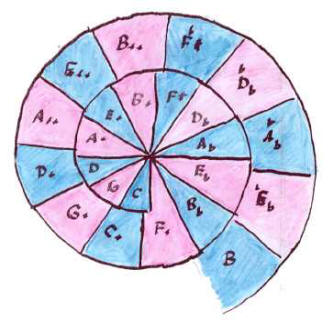As we have already seen, the fifth is the third sound of the series of harmonics, the first being the fundamental and the second its octave. According to the formula of the Tao-te ching, “One has produced two, two has produced three, three has produced all the numbers”, we can understand why the third sound, the fifth, must necessarily produce all the other sounds by its cyclic repetitions. 
←Observe the feminine & masculine notes respectively pink & blue.

The first to be produced will be the four principal sounds, which form comparatively simple ratios with the tonic. 
For the sake of convenience we will use Western notes: See Chinese & Western Music.
I, C 
II, G = 3/2
III, D = 9/8 = (3/2)² * ½ (lower an octave)
IV, A+ ( a comma sharp) = 27/16 = (3/2)³ * ½ (lower an octave)
V, E+ (a comma sharp) = 81/64 = (3/2)⁴ * ¼ (lower 2 octaves). 
These five primart sounds represent the elementary structure of the perceptible world, the pentatonic scale. These sounds are used in music, as you can play the five black keys on the piano. Howevwer, the next two fifths have to be added as two auxiliry sounds:
VI, B+, (a comma sharp) = 243/128 = (3/2)⁵ * ¼ (lower 2 octaves)
VII, L+F? (sharpen a major half tone) = 729/512 = (3/2)⁶ * 1/8 (lower 3 octaves).

The seven-notes Chinese scale

¤ Let us note here that the most striking difference between the system of fifths and that of harmonic relations to a tonic, resides in the perfect fourth, which is an essential interval in the scale of proportions, but in the scale of fifths it is an augmented fourth as its sixth fifth, (3/2) ^6._. 

The two auxiliary sounds – 243/128 and 739/512 – should not be used as fundamentals, though they are needed for transpositions, because they belong to the scale of invisible worlds, and therefore we can neither perceive their accuracy nor build systems upon them without going out of tune.
Instead of starting from C, we could have begun one fifth below, that is to say, from F, and we would have obtained this essential note without changing anything in our scale, except that, since we begin with a masculine interval instead of a feminine interval, the character of the whole system is modified.

The five successive fifths, whether in an ascending or a descending series, represent the limit of consonance in modal music too. Beyond this limit, no interval can appear harmonious, nor can it be accurately recognized. A rule originating from the same principle was also known in medieval Europe, where the tritone was prohibited as diabolical, that is, as connected with forces that are supernatural and therefore uncontrollable. 
Folk music in its pentatonic form had understood this too by only using the span of two fifths up and down.
After these seven notes, the next five notes generated by the series of fifths are: 
VIII, bDb lowered a minor half tone, IX, bAb lowered a minor half tone, X, bEb a minor half tone lower, XI, bBb a minor half tone lower, XII, F+ a comma sharp.

We now have twelve sounds, which divide the octave chromatically into twelve half tones. 
The twelfth fifth (note 13) in a 7 octave span brings us back to the fundamental, but with a slight difference.
It is higher than the fundamental by one comma, the Pythagorean comma (312 / 219 = 531,441/524,288, (5.88 savarts or 23.5 cents). It is, therefore, in our notation, C+, one comma sharp.
In this way, successive series of twelve fifths will be placed one above the other at one-comma intervals, up to the 52nd fifth (note 53) which fill the octave. 

The Chinese continued the cycle of fifths up to 25,524 notes, with a basic interval of 0.0021174 savarts. This cycle is very near to that of the precession of the equinoxes, or the Pythagorean Great Year, which is of 25,920 solar years. Why the Chinese continued so many octaves in the cycle of fifths could have something to do with their reference tone, Kung.

In practice, for reasons that are symbolic as well as musical, after the 52nd fifth (53rd note) the Chinese follow the series only for the next seven degrees, which place themselves above those of the initial seven-note scale, and they stop the series at the 60th note. The reason given is that 12 (the number of each cycle) * 5 (the number of the elements) = 60. 

The scale of 60 Lü

The Chinese scale, being invariable, constitutes in effect a single mode. Every change in expression will therefore depend upon modulation, a change of tonic.
Firstly, the choice of gender: fifths whose numbers in the series are even are feminine. The odd numbered fifths are masculine.
The choice of tonic is dependent on complicated rules and rituals, whose main purpose is to be in accordance with celestial as well as earthly influx or circumstances. Accordingly, the Chinese have to choose the right key for the hour of the day and the month, even during a performance.
It is an extensive scheme, but to get an idea we can say that it corresponds to political matters, seasons, hour of the day, elements, color, geographic direction, planets and moon.
This scale of fifths, perfect for transposition because of its extreme accuracy, also allows the study of astrological correspondences and of terrestrial influx in their Tone Zodiac. 

We notice that the Chinese scale is very similar to the Pythagorean tuning, which was also produced by generating a perfect fifth (3: 2). When the Chinese derived their scale goes back to 3000 BC, when European stone-age man was still beating wooden logs. The prevalent opinion in the West about our music superiority should hereby be moderated.

The Indian music system

The ancient Indians had a less formalized approach to their music than the Chinese. Generally speaking they emphasized the personal inner contemplation more than the outward organized rituals. One can say that they sought inner alignment with the divine supreme by means of the sounds AUM or OM, which were (are) the earthly sound of the prime creator, Brahman. 

For the Hindus, as the Chinese, the spoken or chanted words were the carrier of some of the creative energy, and composed by the prime Creator. Pronounced correctly, it was believed that special words were able to alter humans’ thoughts and feelings and literally change and form physical matter.

Raga is the basic form in classical Indian music. There is a whole system of Ragas, which differ respectively between North and South India. Originally there were only 7 Ragas. These may have been the remnant of an ancient reference to the seven Cosmic Tones: the seven principal notes, or savaras, connected with the seven main planets, and two secondary notes corresponding to the nodes of the moon. This brings the total number of notes in the scale to nine principal notes, which is related to the nine groups of consonants of the Sanskrit alphabet.

The Raga system grants musicians freedom of expression within the limitations of a certain inviolable mode. Since music was so important a force in altering phenomena upon Earth, they considered it would be unwise, dangerous, and perhaps even suicidal in the long run to allow musicians to perform whatever they wished.

The Indian solution was then to apply a system of rules which, while effectively determining what type of music was performed and even its spiritual atmosphere and the period of the day, did not indicate the notes themselves. This was a convincingly successful solution to the problem that the music of ancient civilizations always came up against.

The Chinese had a more rigid system. They created variations by use of instruments, and especially in the expression of the single note. The dimensions of tone color, or timbre, were highly developed in the East. The ear had to learn to distinguish subtle nuances. The same note, produced on a different string, has a different timbre. The same string, when pulled by different fingers, has a different timbre, etc. Furthermore, and very important, the whole spiritual being of the musician himself was crucial. That applies also to Indian music.

As in the Western diatonic scale, the Indian scale was based on 7 main notes: SA, RE, GA, MA, PA, DHA and NI. If we go back to the most ancient texts on music, the scales were divided into two tetrachords, similar to the ancient Greeks, and later put together with a whole tone (9/8) between, Ma – Pa, so a full octave was completed. 
The Indian notes relate broadly to the Western ratios, though the tuning is very harmonious and creates a world of difference. We have to emphasize that the use of harmony as we know it was, but is no longer, musically practised.

Here is a crucial point. The Indian music is modal. There is a strong relationship to the tonic. When a third is played it always relates to the third degree; whereas in Western harmonious tradition the third has a relative position, because it can be the root, the fifth or third of a chord. 
Eastern listeners often make remarks such as: “Beethoven symphonies are interesting, but why have all those chords been introduced, spoiling the charm of the melodies?”
The modal music of India is 'horizontal' as the Western is 'vertical'. The vertical, harmonious system, in which the group of related sounds is given simultaneously, might be more direct though also less clear. The accurate discrimination of the different elements that constitute a chord is not usually possible.

The modal, horizontal system, on the other hand, allows the exact perception and immediate classification of every note, and therefore permits a much more accurate, powerful and detailed outlining of what the music expresses.
One can say that the attention span in the Eastern musical language has to be much longer since, in time, the different and distinct sounds adding up in the listeners mind create the chords or the whole musical idea. Only then, by remembering with attention all the elements that constitute the musical image, can the full meaning finally be understood. 
The Indian musical system operates with a combination of fixed and mutable pitch, so the key can be recognized along with variable notes. The 2nd, 3rd, 4th, 6th and 7th notes are variable, but the 1st (Sa or Do) and the perfect 5th (Pa or Sol) are immutable and of a fixed pitch. The drone is accordingly often Do-Sol (Sa-Pa), which becomes the ultimate open chord containing all other notes within it as a series of subtle harmonics.
This drone (a constant note or tonic), whether actually played on an instrument like the tampura or simply heard within oneself as the Om sound, is the constant reference without which no Indian musician would play.

One must not be confused by the vast use of micro intervals, sliding or bending the notes, prominent in Indian music. The musicians can freely use these microtones as private points, often moving freely between two notes as a kind of infinitely exploitable space, eventually returning home to the tonic of the Raga. The musician has a freedom to play tones as his inspiration demands so long as he obeys the sacred rules of types and its mood.

The 22 Shrutis (degrees)

Musical intervals can be defined in two ways, either by numbers (string lengths, frequencies) or by their psychological correspondences, such as feelings and images they necessarily evoke in our minds. There is no sound without a meaning, so the Indians consider the emotions that different intervals evoke as exact as sound ratios. The feeling of the shrutis depends exclusively on their position in relation to the tonic, and indicates the key for the ragas. 

The 22 different keys or degrees encompass what the Indians consider the most common feelings and reflections of the human mind. They were aware of the division of the octave into 53 equal parts, the Pythagorean Comma, and its harmonic equivalent, the comma diesis, (the syntonic comma, the difference between the major and the minor tones).
However, they chose the 22nd division of the octave for reasons based on the limit of human ability to differentiate the keys, as well as for psychological and metaphysical reasons. The symbolic correspondences of the numbers 22 and 7, (7 strings and main notes), could also play a part since the relationship between the circle and the diameter is expressed as the approximate value of Pi, 22/7.

The modal or Harmonic division of the octave

Indian music is essentially modal, which means that the intervals on which the musical structure is built are calculated in relation to a permanent tonic. That does not mean that the relations between notes other than the tonic are not considered, but that each note will be established first according to its relation to the fixed tonic and not, as in the case of cycle of fifths, by any permutations of the basic note. 

The modal structure can therefore be compared to the proportional division of the string (straight line) rather than to the periodic movement of the spiral of fifths.
All the notes obtained in the harmonic system are distinct from those of the cyclic system, which is based on different data. Though the notes are theoretically distinct and their sequence follows completely different rules, in practice they lead to a similar division of the octave into fifty-three intervals.

The scale of proportions is made of a succession of syntonic commas, 81/80, which divide the octave into 53 intervals. Among those, 22 notes were chosen for their specific emotional expressions:

The Ancient Egyptians

The ancient Egyptians had similar beliefs to the Chinese and Hindus. In their Book of the Dead and other sources, it is stated that God, or his lesser servant gods, created everything, by combining visualization with utterance. First the god would visualize the thing that was to be formed; then he would pronounce its name: and it would be. 

From as late as the reign of Alexander II, a text dating from about 310 BC still has the God of Creation, Ra, declaring: “Numerous are the forms from that which proceeded from my mouth.” The god Ra was also called Amen-Ra, with the prefix ‘Amen’. The Egyptian priesthood understood well the word Amen, or AMN, and it was equated with the Hindu OM.

Egyptian music, as does Greek, most probably had its roots in Indian music, or at least in that universal system of modal music whose tradition has been fully kept only by the Indians. 
The pyramid can easily be a symbolic representation of Earth with its four perceptible elements, and all its characteristics that are regulated by the number four – the four seasons, four directions of space, etc.; especially the projection of the single into the multiple.

WESTERN MUSIC
Pythagoras

The Greek philosopher Pythagoras (570 - 490 BC) spent 22 years in Egypt, mainly with the high priest in Memphis, where he became initiated into their secret knowledge of Gods. When the Persians conquered Egypt, he was kept in captivity in Babylon for sixteen years before he could return to Greece and begin his teaching. 
I began to study the theory of the Pythagoreans and their esoteric schools. Very little is known of them. Pythagoras demanded silence about the esoteric work. This historic school was founded in the Greek colony Kroton, in southern Italy, about 2,500 years ago.

I realized after reading dozens of books about the matter what an outstanding role that school played in the establishment of western civilization. He created an entirely new concept. Any person - man or woman - who had a sincere wish for knowledge could enter the school stepwise, with a number of initiations. The tradition of a priesthood’s monopoly of knowledge of God was broken.

Pythagoras' study of the moving string and his discovery of the harmonic progression of simple whole numbers was the first real scientific work and creation of modern science. But his vision went far beyond present science in his deep understanding of the integration of the triad: A – science, B – work on being, C – love and study of God. Something modern science could learn from!

Nicomachus of Gerasa

Nicomachus the Pythagorean (second century B.C.) was the first who wrote about Pythagoras’ legendary encounter with ‘the harmonious blacksmith’ and the weights of the 4 different hammers being 12, 9, 8 and 6, that determined the variation in the pitches Pythagoras heard.
This story illustrates how the numerical proportions of the notes were discovered. His methodical measuring of the hammers and how the sound was produced and related (collecting data), then making experiments with strings, their tension and lengths (repeating the findings and, with mathematics, formulating them into a law), was the first example of the scientific method.

We will not dwell on the question of the force of the impact or the tension of the strings, which later was discovered as the square root of the force, but just stick to the proportion of weights and the pitches he heard, which led him to his discovery.
Pythagoras' experiments led to the combination of two tetrachords, (two fourths), separated with a whole tone, 9/8, which constitute an octave. He changed the traditional unit in Greek music, the tetrachord, into the octave by an octachord.

In the time of Pythagoras the tradition was strongly based on the seven strings of the lyre, the heptachord. The Greeks considered the number 7 sacred and given by the god Hermes, who handed down the art of lyre playing to Orpheus. The seven-string lyre was also related to the seven planets, amongst other things the ancients venerated.
The lyre often, but not always, consisted of seven strings comprising two tetrachords, each one spanning the most elementary concord, the fourth, both joined together on the note mese.

According to legend, a son of Apollo, Linos, invented the four-stringed lyre with three intervals, a semitone, whole tone and a whole tone comprising a fourth; the fourth, ‘the first and most elementary consonance’ as Nicomathus calls it, and from which all the musical scales of ancient Greek music eventually developed.
Trepander of Antissa on Lesbos, born about 710 B.C., assumed a mythological status for his musical genius. His most lasting contribution was perhaps his transformation of the four-stringed lyre to the instrument which became institutionalized by tradition to the heptachord.
Trepander did before Pythagoras extend the heptachord from its minor seventh limits to a full octave, but without having to add the forbidden eighth string.
He removed the Bb string, the trite of the conjunct tetrachord, and added the octave string, E1, yielding a scale of E F G A C D E1.
This arrangement left a gap of a minor third between A and C, and seemed to have enhanced the Dorian character of Trepander's composition. 

Harmonia

Only Pythagoras escaped censure for adding an eighth string to the ancient and venerated lyre because of his position as a great master and religious prophet. His purpose was to teach man the unifying principle and immutable laws of harmonia by appealing to his highest powers - the rational intellect and not to his untrustworthy and corruptible senses. Pythagoras altered the heptachord solely to engage man's intellect in proper ‘fitting together’ - harmonia - of the mathematical proportions.

Plutarch (44-120 B.C.) states that for Pythagoras and his disciples, the word harmonia meant ‘octave’ in the sense of an attunement which manifests within its limits both the proper fitting together of the concordant intervals, fourth and fifth, and the difference between them, the whole tone. 
Moreover, Pythagoras proved that whatever can be said of one octave can be said of all octaves. For every octave, no matter what pitch range it encompasses, repeats itself without variation throughout the entire pitch range in music. For that reason, Pythagoras considered it sufficient to limit the study of music to the octave.

This means that within the framework of any octave, no matter what its particular pitch range, there is a mathematically ordained place for the fourth, the fifth, and for the whole tone. It is a mathematical matter to show that all of the ratios involved in the structure of the octave are comprehended by the single construct: 12-9-8-6. 
For the Pythagoreans, this construct came to constitute the essential paradigm - of unity from multiplicity.

The arithmetic and harmonic mean

We see that 12:6 expresses the octave, 2:1; 9 is the arithmetic mean, which is equal to the half of the sum of the extremes, (12 + 6)/2 = 9.
Further, 8 is the harmonic mean of 12:6, being superior and inferior to the extremes by the same fraction. 
Expressing this operation algebraically, the harmonic mean is 2ac/a+c, or in this series, 2*12*6/12+6 = 8. 

Among the peculiar properties of the harmonic proportion is the fact that the ratio of the greatest term to the middle is greater than the middle to the smallest term: 12:8 >8:6. It is this property that made the harmonic proportion appear contrary to the arithmetic proportion.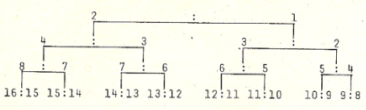

In terms of musical theory, these two proportions are basic for division of the octave since the fifth, 3/2, is the arithmetic mean of an octave and the fourth, 4/3, is the harmonic mean of an octave.
The principle of dividing the string by an arithmetical proportion is done by the formula: a:b is divided by 2a:(a+b) and (a+b):2b.

The ancient Greeks presumably did such division in their studies of the singing string of the monochord.

The semitone

We have already seen that in the diatonic genus each tetrachord was divided into two full tones and one semitone. A full tone derives from a fifth minus a fourth, 3/2 - 4/3 = 9/8. The semitone will be 4/3 - (9/8 + 9/8), or 4/3 - 81/64 = 256/243. 
This semitone is called leimma, and is somewhat smaller than the half tone computed by dividing (for musical ratios dividing means the square root) the whole tone in half: (9/8)^½ = 3/2*2^½.

The square root of 2 was for the Pythagoreans a shocking fact, because their concept of rational numbers was shattered. (For me it represents the beauty of real science, because it revealed the flaws in the Pythagorean paradigm of numbers). Their own mathematic proved with the Pythagoreans’ doctrine of the right-angle triangle (the sum of the squares of the two smaller sides of a right-angled triangle is equal to the square of the hypotenuse) that in music, as in geometry, there are fractions, m/n, that are incommensurables – such as the square root of 2, which cannot be expressed with whole numbers or fractions, the body of rational numbers, but with irrational numbers not yet developed.
This discovery was held as a secret among the Pythagoreans and led to the separation of algebra and geometry for centuries, until Descartes in the 17th century united them again.

For music it meant that there was no center of an octave, no halving of the whole tone, no perfect union of opposites, no ‘rationality’ to the cosmos. 
The semitone could be the ‘door’ to other dimensions!

My task here is to give some clues to the meta-physical functions of semitones, which seem to involve the potential to shift to a different world or enter another dimension. The key to attaining a different spiritual world exists in the search for the exact right tone that resonates with that particular ‘door’ to other dimensions and worlds. The human being contains more dimensions than just three spatial dimensions. 

Philolaus

We have to bear in mind that Pythagoras himself left no written record of his work; it was and is against esoteric principles. Neither did those few students who survived the pogrom of Pythagoras. It is one in the next generation of Pythagoreans, Philolaus (ca.480- ? B.C.), who broke the precept of writing down the master’s teaching. However, Philolaus' records are lost, so it is Nicomachus’ fragments of his writing, in his Manual of Harmonics, that is actually the only source posterity has.

According to Nicomachus / Philolaus, the whole tone, 9/8, was divided differently from the Pythagoreans method, by representing the whole tone with 27, the cube of 3, a number highly esteemed by the Pythagoreans. Philolaus divided the whole tone in two parts, calling the lesser part of 13 units a ‘diesis’, and the greater part of 14 units, ‘apotome’. Philolaus had, in effect, anticipated Plato's calculations in the Timaeus!

Timaeus by Plato

Plato (427-347 B.C.) gave in his work Timaeus a new meaning to the Pythagorean harmonic universe by – in a purely mathematical method – enclosing it within the mathematically fixed limits of four octaves and a major sixth. It was determined by the numbers forming two geometrical progressions, of which the last term is the twenty-seventh multiple of the first term:
27 = 1+2+3+4+8+9
The two geometric progressions in which the ratios between the terms is 2:1 and 3:1 are, respectively:
1-2-4-8 and 1-3-9-27.
Combining these two progressions, Plato produced the seven-termed series: 1-2-3-4-8-9-27. The numbers in this series contain the octave, the octave and a fifth, the double octave, the triple octave, the fifth, the fourth and the whole tone. The entire compass from one to twenty-seventh multiple comprises, therefore, four octaves and a major sixth. In numerical terms it contains four octaves, 16:1 * 3:2 (a fifth) * 9:8 (a whole-tone) equals 27:1.
Plato then proceeded first to locate in each of the octaves the harmonic mean, the fourth, then the arithmetic mean, the fifth. By inserting the harmonic and the arithmetic means respectively between each of the terms in the two geometric progressions, Plato formulated mathematically everything Pythagoras had formulated by collecting acoustic data.

Plato did, however, independently of the Pythagoreans, compute the semitone in the fourth, which consists of two whole tones plus something, which is less than the half of a whole tone, namely 256:243, the leimma.
According to Flora Levin in her commentary on Nicromachus' ”The Manual of Harmonics”, Plato went further than Pythagoras by completing all the degrees in a diatonic scale:

Plato's calculations led to the inescapable fact of no center to the octave, no halving of the whole tone with rational numbers, no rationality of the cosmos.
Nicomachus did his part in covering up the secret by misrepresenting Plato and putting off some of the shattering discoveries of irrational numbers to some future time.

The semitones in the different modes

Pythagoras had practiced music long before he transformed the heptachord into an octachord that led him to discover the mathematical laws determining the basic structure of an octave. He had fully understood the therapeutic value of music in healing the body and soul. Most of all, he knew the set of conditions for melody. He recognized strongly that every tetrachord on which melody was based embodies the ‘natural’ or physical musical progression of whole tone-whole tone-semitone. 
He maintained the fundamental structure of both tetrachords in his scale, and for musical reasons he understood that this distribution of intervals had to be maintained for all melodic purposes with their configurations and inversions.
This was the foundation of the ancient Greek music, which further developed into The Greater Perfect System.

The confusion of systems

The Greek music has an inherent confusion of musical systems: a mix of the cyclic system of perfect fifths (Pythagorean tuning), and the modal system (tetrachords). We can only get a very faint idea of what ancient Greek music really was about because European theorists through time have made errors and misunderstandings. 

In reality, the Arabs and the Turks happened to receive directly the inheritance of Greece. In many cases the works of Greek philosophers and mathematicians reached Europe through the Arabs. Most serious studies on Greek music were written by Arab scholars such as al-Färäbi in the tenth century and Avicenna a little later, while Westerners - Boethius in particular - had already made the most terrible mistakes. 
It is the Arabs who maintained a musical practice in conformity with the ancient theory, so to get an idea of ancient Greek music, we should turn to Arab music.

The Pythagorean Tuning

The musical scale, said to be created by Pythagoras, was a diatonic musical scale with the frequency rate as:

This scale is identical to the Chinese cyclic scale of fifths, if we take F as the tonic.
 It has 5 major tones (9/8) and 2 semitones, leimma (256/243), in the mi-fa and si-do interval.
The third, 81/64, is a syntonic comma sharper than the harmonic third, 5/4.
Here is the seven-notes Chinese scale:

¤ Let us note here that the most striking difference between the system of fifths and that of harmonic relations to a tonic resides in the perfect fourth, which is an essential interval in the scale of proportions.
The scale of fifths has an augmented fourth as its sixth fifth, (3/2). 

The Pythagorean scale was based on the three prime intervals: the octave, the perfect 5th and the perfect 4th. “Everything obeys a secret music of which the ‘Tetractys’ is the numerical symbol” (Lebaisquais).
By generating 12 perfect fifths in the span of 7 octaves, 12 tones were produced. In order to place the tones within one octave, the descending perfect 4th (the subdominant) was used, and a 12-note chromatic scale was made.

He discovered what later was called the Pythagorean comma, the discrepancy between 12 fifths and 7 octaves gives (3:2)¹² > (2:1)^7. Calculated through, it is: 129.74634 : 128 = 1.014. Or in cents: 23.5. Do not mistake Pythagoras' Comma for the syntonic comma, equal to 22 cents, which is derived from the difference between the major tone and the minor tone in the Just Diatonic Scale, or discrepancy between the Pythagorean third and the third in the harmonic series which is 5:4.

As far back as 2,500 years ago the Pythagorean figured out that it was impossible to derive a scale in which the intervals could fit precisely into an octave. The ancient Greeks explained this imperfection – the comma – as an example of the condition of mortal humans in an imperfect world.
This fundamental problem with the 3 prime ratios: 2:1, 3:2, 4:3 – which can be formulated in mathematical terms as interrelated prime numbers having no common divisor except unity – has been compromised in a number of different temperaments of the diatonic scale up to our time.

In ancient Greek music several other modes were used based on the tetrachords with a span of the perfect fourth. Later, two tetrachords were put together with a full tone in between so an octave was established. A number of different modes were used in practical music performance. The different placement of the two half tones made the different modes.
An account of ancient Greek contributions to musical tuning would not be complete without mentioning the later Greek scientist Ptolemy (2nd C. A.D.). He proposed an alternative musical tuning system, which included the interval of the major third based on that between the 4th and 5th harmonics, 5 / 4. This system of tuning was ignored during the entire Medieval period and only re-surfaced with the development of polyphonic harmony.

Gregorian church music

From those ancient Greek modes the Christian Gregorian church derived its music, though their names were a complete mix-up of the original Greek names for their modes. What is important in this context is the placement of the two semitones in the octave. They were placed differently in order to create different modes that produced a special tonality or mood. The interaction between tones and semitones made each characteristic mode.
The Gregorian church music from the late Middle Ages developed an amazing beauty and spirituality. We owe the monks – and Hildegard von Bingen - a debt of gratitude for their part – singing to worship the refinement of the soul and Divinity.
A side effect was the healing power in the strong proportion of higher harmonics, which invigorating effect Alfred Tomatis has described in my page The Power of Harmonics.

As long as musical practice was mainly monophonic, the number of scales could be many. When the wish for harmonious polyphonic singing was appearing, the elimination of scales began because only the scales that were in agreement with the harmonics could be used.

Polyphonic music

The development in musical practice from monophonic to polyphonic, and after the Renaissance (the end of 15th century) to harmony, made it necessary to have especially the third harmonized. The Pythagorean third (81:64) is a syntonic comma larger than the harmonic third (5:4). The need for harmonizing the third in the part-songs became imperative as the polyphonic music became predominant.

Just Intonation - a scale of proportion

Since the major triad became the foundation of harmony in Western music, the Pythagorean scale has largely been discarded in favor of the Just Diatonic Scale, or the scale of Zarlino (1540-94). 
The frequencies of the notes in a root position major triad are given by the fourth, fifth and sixth harmonics in the harmonic series, i.e. the frequencies should be in the ratio 4: 5: 6. (1-5:4-3:2).

The Major Triad as a generator

If we look at this triad as C, E, and G, the tonic triad, and associate it with its dominant G, B, D and the tonic’s sub-dominant F, A, C, each of which has one tone in common with the triad of the tonic, we obtain the complete series of tones for the major scale of C:

This scale consists of three different intervals: major tone 9/8, minor tone 10/9, and major half tone 16/15. Therefore, when the tonic is changed, we shall obtain sharps and flats of different nature in order to keep the frame of the scale, and the very notes of the original scale will in some cases have to be raised or lowered by one comma (the difference between the major and the minor tone).
Those who are familiar with Rodney Collin's The Theory of Celestial Influence will notice that the Just Intonation is the scale he applies to his great work on octaves by multiplying by 24.

The scale of Zarlino (Just Intonation) is basically a mix of notes generated by fifths, which allows right transpositions and notes which make correct harmonic intervals; so in practice, two different systems are used conjointly, which results in awkward transpositions. 

The Mean Tone

In musical practice, especially when playing with key-instruments or the simple modulation of keys, the Just Intonation causes many difficulties, mainly due to the fact of the major and minor tones. The two different intervals of a tone in this scale was for that reason modified during the 17th century into a mean or average of the major and minor tone. Since these two tones together equal a major third, the mean tone is equal to half of the major third, or 193 cents.

This temperament is not surprisingly called Mean Tone temperament, or 1:4 comma mean tone (the fifths are all equal, but have been tempered by 5.5 cents, a quarter of a syntonic comma) and was the most used temperament in Baroque music.

There were some problems with the enharmonic notes. The two diatonic semitones do not add up to give a (full) tone. The Mean Tone semitones are 117.5 cents. So if one wishes to play in more than six major and three minor keys, there is trouble. This is because en-harmonically equivalent notes will not have the same frequency. Additionally, this temperament has some real false notes, called ‘wolf notes’, due to the 3.5 cents short fifth, so the circle will fall short of closure by 12 x 3.5 cents = 42 cents.

Equal Temperament

The ultimate compromise appears in Equal Temperament, which is a circular temperament. The Pythagorean comma (as approximately 24 cents) made the circle too large. If the 12 perfect fifths –702 cents – are equally distributed but contracted with 2 cents each, the circle of fifths will be complete into a circle.
In the late 17th and 18th centuries a number of circular temperaments were employed making use of this device. It is often said that J.S. Bach's 48 Preludes and Fugues were written to demonstrate the effectiveness of Equal Temperament. However, recent research (Barnes 1979) has shown that he probably wrote them for a circular temperament similar to one devised by Werckmeister (known as Werckmeister III), where the distribution of fifths was unequal; some were 6 cents smaller, some were perfect.

The Equal Temperament as we know it is completely equally distributed, slightly diminished fifths (700 cents), that at one blow eliminates the question about different frequencies of the enharmonic notes and modulation limitations.
The octave is equally divided into 12 semitones of 100 cents. The frequency ratio for each of the semitones is the twelfth root of an octave: (2/1) 1/12 = 1.059463094.../1.

This temperament has two scales, a major and a minor. The difference lies in the third, sixth and seventh, which are a half tone lower in the minor scale. Note that the same intervals are present in the minor scale as in the major scale, although the order is different.
We will not deal with the harmonic minor scale or the melodic minor scale.

Let us make a comparison in cents of the above mentioned scales with the Just Diatonic Scale (Just Intonation) as base:

In the western culture Equal Temperament is now so established and its tonality so tuned in our ears, that it sounds just right, though the third and the sixth ought to give problems because they are pretty much sharper than the much purer and expressive Just Intonation.

The artificial Equal Temperament

The great German scientist from the 19th Century, Hermann von Helmholtz, who was also a capable musician, made a strong stand for the Just Intonation scale. He claimed in his On the Sensations of Tone that... “continual bold modulational leaps threaten entirely to destroy the feeling for tonality.” Further he states: “The music based on the tempered scale must be considered as an imperfect music... If we suppose it or even find it beautiful, it means that our ear has been systematically spoiled since childhood.”

Professor Helmholtz brought many examples of beautiful use of Just Intonation in singing by use of the English system ‘Tonic Sol Fa-ists’, which overcame the difficulties of modulation by using a different musical notation system. Strings and wind instruments could also perform this; so can modern keyboards.
The discussions about Equal Temperament versus Just Intonation have continued up to present time. Daniel White has on his web page Tuning & Music Scales Theory made an in-depth analysis of this matter, concluding that ET sounds ‘sweeter’ than JT.

Compared with the other scales we have gone over, the Equal Temperament has no definite relations between the sounds since it has lost its relationship with simple ratios. The more complicated the ratios are, the more dissonant are the chords. We have been used to the muddy sounds, but people in the East who are trained in modal memory and clear harmonic relations cannot conceive the meaning of Western music.
The Equal Temperament has, in spite of its obvious weakness, made it possible for great composers to create beautiful music with extraordinary numbers of new chords and modulations. 
In the twentieth Century the tendency to move away from simple ratios between notes to sound ratios even far away from Equal Temperament became manifest in atonal music.

Modern Dodecaphonic music

In modern times a number of atonal scales has been developed to serve the new dodecaphonic music (Schönberg, Berg, Webern), where the classical notion of harmony and rhythm is dissolved. Basically, the ancient diatonic scale with its five whole tones and two semitones has been replaced with a pure chromatic scale, which is a main factor in the change from melodic tonal music to atonal dodecaphonic music.
Though I am very fond of non-figurative art, the modern atonal music is still difficult for me to enjoy spontaneously. Educated people assure me of the new beauty in contemporary music, which I can hear with my head, but not with my heart.
I have, however, observed a certain indifference in the mainstream of classical music, and find myself attracted to the early European music and folk (World) music.

My main objection to the atonal dodecaphonic music lies in its detachment from the physical world. The scale belongs to the invisible realm because it is created by ratios far away from the small numbers, which are related to the perceptible world and basic emotions. 
In the ancient musical systems we have seen how closely the musical scale had to be related to the perceptible world represented mainly as small numbered ratios (low number of generating fifths in the cyclic system or simple harmonic ratios in the modal system).

Cyclic and modal numbers

In this world of five elements in which we live, no prime number higher than five can enter into a system of sounds representing melodic or harmonic relations. The Chinese system of cyclic fifths even refuses to get beyond this number five; all its intervals are expressed in terms of powers of two or three. The number for cyclic systems is three.
Some modern theorists are using the terms ‘3 limit scale’and ‘5 limit scale’.

The introduction of the factor of five brings us to the harmonic modal scale, of which the characteristic intervals are the harmonic major sixth, 5/3, the harmonic major third, 5/4, the minor third, 6/5, the major half tone, 16/15 (24 /3*5), the minor half tone, 25/24, (52 /3*23 ) the syntonic comma, 81/80, (34 / 24 * 5), and so forth.
Compared with the Equal Temperament, the tempered half tone is something like 1,059,463,094 / 1,000,000,000 against the major harmonic half tone 16/15.

The number five ‘humanizes’ the music. It makes the music an instrument of expression of tangible reality. The introductions of higher prime numbers, such as seven, would take us beyond this reality into regions that are not within the scope of our normal perceptions and understanding.
Seven is considered the number of heavenly as well as infernal regions. We have actually no means of knowing to which side it may lead us!

In my opinion you can only touch humans deeply if you play harmonious or tonal music, because these tones belong to the real world and the man who walks the Earth. The scale has to be more or less in accordance with the lower harmonics in the series. The way we hear and analyze sound is actually much the same as the standing wave in a string. The basilar membrane in the inner ear behaves like a ‘string’, and the ‘software’ in the brain is designed to look for the harmonic series. It is the most agreeable - and most basic. What it all comes down to is that the only measure for all phenomena is the human.

Reference tone

Before a concert begins, a reference tone, the concert pitch, is played so the instruments can tune their middle a'. In modern times the pitch was set to 440 Hz. by the second International Standard Pitch Conference in London 1938. It is a high pitch compared to the older concert pitch of 435 Hz., which was introduced by the French government in 1859 in cooperation with musicians such as Hector Berlioz, Meyerbeer and Rossini.
The concert pitch has varied in earlier times, depending on country and time. In the book On the Sensation of Tone by Helmholtz, a record of concert pitch in Europe covers many pages. The characteristic for Western music is that concert pitch is arbitrary. It has no relation to forces above man. There is no reference to earthly or celestial influx, but only to an artificial standard.

For the old Chinese the tuning of their fundamental tone, Kung, was a matter of utmost importance for their civilization; it had to be in alignment with the Cosmic tone so the celestial influence could be channeled into society by music. 

We earlier mentioned Cousto's calculations (in his book The Cosmic Octave). He relates the Kung to the frequency of the Platonic Year. The note of the Platonic year is found to be F in Western Equal Temperament pitch, which is in the 48th octave with a frequency of 344.12 Hz.

The Indians’ method had the character of meditation, since the musician not only has to tune his instrument to the keynote in the prelude, he also attunes himself to it, and gives the audience the opportunity to do so too. This long introduction is essential since the musicians have to tune in to the ‘sadja’, the everlasting, never-ceasing tone. According to Indian tradition it stands for primordial vibration, which is called ‘nada’ and expresses the universal OM.

The OM sound, according to Cousto, corresponds approximately to the C sharp in the small octave of the present day tuning system (136 Hz), and to the 32nd octave tone of the Earth year. It means that in lowering 136 Hz tone by 32 octaves, the resulting frequency will be as slow as the amount of time it takes the Earth to circle the sun.

It is interesting to note that the Indians arrived at this tone, which we can calculate mathematically, ‘simply’ through intuition and meditation.
(The calculation is: A day consists of 86,400 seconds. A tropical year has 365,242 days = 31,556,925,9747 seconds. The reciprocal value multiplied by 232 = 136,10221 Hz.)
Concert pitch in western music, which is 440 Hz for the middle A, ought to be 435,92 Hz based on the note corresponding to the average solar day, according to Cousto.

“It don't mean a thing, if it ain't got that swing”
Those who are familiar with the jazz (swing) musician, Duke Ellington, will ‘hear’ Ella Fitzgerald sing this song. The reason I will end on that note is to make clear that music is more than scales and right tuning. Music contains of four major elements:
Melody, Rhythm, Harmony and Interpretation or Intention.

Having this in mind I will continue with The Sound of Silence, where I will extend the law of octaves into realms other than scales and tuning by an elaboration on the metaphysical properties of sound and music.

Thomas Váczy Hightower © 2002-9.

Send me a comment: mail@vaczy.dk

Index page
References and literature.