Hans Cousto was the first to calculate the frequency of the sun (1981), which has to be theoretical since we are not able to measure the orbiting speed of the sun from our position in the universe.
As he wrote in his book, The Cosmic Octave, he got the clue in his study of Johannes Keples works. Cousto was looking at the log-log graph of the solar system displayed below.
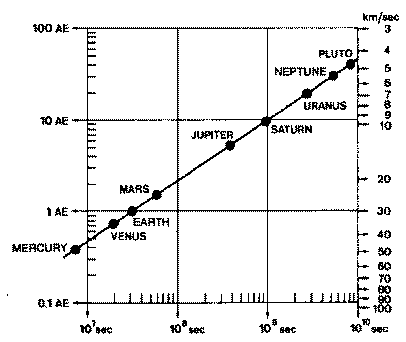
The straight line represents a function existent between orbit, orbital speed,
and mean distance from the sun. Kepler formulated this function in his third law
of planetary motion, which states that the ratio of the square of the revolution
period to the cube of the major orbital axis’s, is the same for all planets.
It was the origin of this straight line, that made Cousto think, that this kind of order does not only apply to the solar system, but to any similar systems, so where would the limit be if a similar situation were depicted in such a graph?
The limit in orbital speed should be the speed of light, so the calculation would be to find how long it would take a “planet” to move a speed of light to orbit the sun, and how great its mean distance to the sun would be.
Cousto’s
calculation is displayed in the appendix, and I do not have skills to question
the calculations, that is based on Einstein's general theory of relativity, so I just quote his
findings regarding the frequency of the sun:
Orbital
speed = speed of light.
Mean distance to
the sun: 1,476,625 km. (The distance to the theoretical planet to the centre of
the sun, would correspond exactly to the gravitational length of the sun).
Period of
revolution around the sun: 0.030 95 sec.
Frequency of the period of revolution: 32 312 Hz.
Edited by Thomas Hightower.