The
Creation of Musical Scales, part I
from a mathematics and
acoustic point of view,
by Thomas Váczy
Hightower.
The focus will
be on the acoustic laws behind the musical scales and how numbers and
mathematics play a part in creating the intervals in the octave.
Which factors have significance for creating a musical scale? Why is
the division of the octave so basically common in different musical
traditions, and what make them differ? Why is the ancient Greek
Pythagorean scale basically identical with the old Chinese scale?
What causes the modern Western musical scale, the Equal Temperament,
to be ‘disharmonious’ compared to the Eastern scales?
Music has often played an important part
in shaping a culture. Some say that music is the hidden power in a
culture. In ancient societies it was considered a serious public
matter, a foundation for the culture. The musical scale itself
and the right tuning of intervals can make all the difference as to
how chaos or order. It also ensures that humans are in accord with
earthly as well as celestial influence.
The more metaphysical aspects of
music and sound and its influence at the level of consciousness and
healing can be studied in my second part, The
Musical Octave II, where I will mix different levels and
categories into a larger picture.
In this thesis I will perform an
analysis of four different musical traditions and their basic
scales:
·
the ancient Chinese
·
the Indian musical tradition
·
the old Greek music
·
the following European musical scales.
By looking at the many tuning
systems worldwide, one common factor is outstanding, the octave.
The word derives from Latin and means ‘eighth’. It is
the 8th step in the diatonic scale consisting of 7 tones, containing
5 full tones and 2 semitones. The eighth tone in the diatonic scale,
which is the most common in the world, completes the octave on a
pitch that in frequency is the double of the fundamental tone.
This universal unit, that divides the
realm of sound by the factor 2, can be subdivided in three basic
ways:
1) By a geometric
progression, with any number of equal intervals, such as the
common Western mode, the Equal Temperament with 12 semitones, and
other numbers.
A geometric progression is a sequence in
which each term (after the first) is determined by multiplying the
preceding term by a constant. This constant is called the common
ratio of the arithmetic progression. The octave sequence is a
geometric progression; so is the golden section.
2) By proportions
with low number ratios, e.g. Just Intonation with its triads
of major Thirds, or by other harmonic relations to the tonic (Modal
music), e.g. Pentatonic or Septonic (e.g. Indian music).
Systems
of proportions are used in Modal music, e.g. the harmonic mean and
the arithmetical mean in the division of an octave.
3) By generating
Fifths, e.g. Pythagorean Tuning or The Chinese Scale.
There
are hybrids too, such as the Mean Tone Temperaments.
The habits
of hearing
The reason there are so many different
ways to divide the octave and display such a range of scales can be
found in the fact that there are no formula that can fit the octave
perfectly. The different ratios expressed in numbers are prime
inter-related, so a common divisor is not possible in an octave -
unless some notes or keys are sound disharmonious.
Different
musical traditions embrace this schism depending on what they
consider best fit for their musical expression. The culture in which
the musical scale has emerged is a profound reflection of that
particular culture.
The Eastern music tradition considers
the fine-tuned intervals of much more importance than the Western,
which prefers first harmonious chords in any key. Consequently there
are intervals which are perceived as consonant in the West, but
considered dissonant in the East.
What it comes down to is habits. A
musical scale is deeply ingrained. It shapes the way one hears tones
in succession in a fixed pattern. There have to be at least
three elements in defining a mode, just as three notes are needed to
define a chord.
In the modulating cyclic systems, where
every sound is mobile, it is necessary to repeat the ‘body of
harmony’ (tonic, fifth or fourth and octave) in order to
establish the meaning or mood of the note, but in the modal system
one note alone, by changing its place, can produce the effect of a
chord.
The modal frame, being fixed and firmly established in the
memory of the listener, has no need to constantly repeat chords as in
harmonic music, in order to express the numerical relationship.
That
shape of ingrained intervals goes more or less out of tune, when
changes of key or transposition moves the frequencies up or down. It
is the way enharmonic notes arise. Increasing pitch by a half tone is
not the same as decreasing by a half tone. They are two different
notes.
Expressed graphically, the frequencies’
ratios behave exponentially - in a non-linear curve - (which is
displayed e.g. by the logarithmic spacing of the frets on the neck of
the guitar), so a discrepancy is produced by moving the set frame up
or down. This discrepancy is expressed in the different ‘commas’,
such as the Pythagorean comma or the smaller Syntonic comma (the
comma of Didymos).
The notion of harmony is different too.
In the West the perception of harmony is ‘vertical’ -
meaning as chords played at once. The Eastern tradition of harmony is
‘horizontal’. Each tone is carefully played, and by
attention over time adds up in the memory to harmonious chords.
Laws of acoustic
Before we deal with the creations of
musical scales, we have to dwell on the underlying foundation of
scales, namely the physical laws of sounds.
Acoustics is a branch
of physic that is complicated and extensive, so I have only chosen -
in a brief form - those parts we need to look at in order to
understand the invention of musical scales.
Sound is vibrations, but three
conditions have to be in place, if a sound is to be heard:
1) The
vibrating source for the sound – an oscillator.
2) A medium
in which the sound can travel, such as air, water or soil.
3) A
receiver for the sound, such as a functional ear or a microphone.
The sound wave is a chain reaction where
the molecules of the medium, by elastic beats, push the other
molecules in a longitudinal direction - quite like a long train
getting a push from a locomotive.
It is a longitudinal
displacement of pressure and depressor in a molecular medium such as
air or water. Any sound is initiated by an oscillator, which can be a
huge range of devices and instruments, each one having its own
definite characteristic sound.
The sound waves should not be imagined
as waves in water caused by e.g. a stone in a pond, though the
picture appears to be alike.
Sound waves are longitudinal:
pressure waves - back and forth.
Water waves are transverse:
the main movements are up and down in a circular motion.
Please
note that longitudinal pressure waves will reappear in the
description below of logarithmic, standing pressure waves.
Moving
string
Plucked strings exhibit transverse
waves in a back and forth movement, locally producing a pulse along
the direction in which the wave itself travels, with a speed
depending on the mass of the string and its material but usually
lower than airwaves. (A good explanation is given by The
University of New South Wales, Australia.)
The frequency of the string itself is
the same as the frequency of the air waves. The wavelength is
different due to the dissimilarity in speed.
The length of the
vibrating part of the string is in inverse proportion to the
frequencies. The period of oscillation = 1 / frequency. This is an
important acoustic law that applies to any conversion of period into
frequencies. If, for example, you divide an octave string by 2/3, the
ratio of the sound will be 3/2 of an octave, a fifth.
Oscillators
 To
produce sounds, a vibrating body, an oscillator,
is needed.
To
produce sounds, a vibrating body, an oscillator,
is needed.
An oscillator can be any kind of a vibrating body from
an atom to an astronomical object, but since we are here working with
musical sounds, we are referring to oscillators such as musical
instruments or the human voice box, that produce standing waves or
periodic waves in a system of resonators that enhances and amplifies
the tone and generates harmonics.
The heart and aorta form a
special resonant system when breathing is ceased. Then the heartbeat
seems to wait until the echo returns from the bifurcation (where the
aorta forks out in the lower abdomen). Then the next heart beat sets
in. In this synchronous way a resonant, standing wave of blood is
established with a frequency of about seven times a second. This
harmonious mode requires for its sustenance a minimum amount of
energy, which is an intelligent response from the body. In deep
meditation a similar mode is established. It is interesting to notice
that this mode of 7 Hz is close to the Schumann resonance.
Standing
waves
Standing waves are a kind of echo that
moves back and forth, since the waves are reflected between two solid
points, basically, a or fixed string. For wind instruments with an
open end, the impedance (the resisters from the air) works in a
similar manner. There are also closed pipes that resonate a bit
differently.
 When
a fixed string is plucked, the potential energy is released in a
transverse wave, that in a split second begins to initiate a division
of the string into different moving parts, where some points are not
moving. These stationary points are called nodes. How
many nodes the string is divided into when it vibrates depends on the
material, the tension, and especially how and where it is plucked or
bowed, etc. But here we try to get a general picture of the nature of
standing waves in a plucked string.
When
a fixed string is plucked, the potential energy is released in a
transverse wave, that in a split second begins to initiate a division
of the string into different moving parts, where some points are not
moving. These stationary points are called nodes. How
many nodes the string is divided into when it vibrates depends on the
material, the tension, and especially how and where it is plucked or
bowed, etc. But here we try to get a general picture of the nature of
standing waves in a plucked string.
When the potential energy is
stopped at the fixed ends, the kinetic energy is at its maximum and
continues in a 180° phase
shift the opposite way. We thus have two waves with the same
frequency and amplitude traveling in opposite directions. Where the
two waves add together or superpose, movement is canceled out and we
have stationary nodes that occur a half wavelength apart and
constitute the standing waves.
The repeating shifts between potential
and kinetic energy in a moving string draws one’s attention to
a similar pattern we can observe in a pendulum and its simple
harmonic motion.
The numbers of nodes,
the non-moving points in a standing wave, is equal to the number of
harmonics or partials created in the
standing wave.
The same pattern can be observed with
fine sand on a metal plate set in vibration by a bow. The standing
waves automatically divide the length and width of the plate into an
integral number of half wave-lengths. It is only then that a standing
wave can be sustained. That pattern is the most energy-effective form
nature can provide. (A similar pattern is the rhythm entrainment,
where random oscillations after a while begin to oscillate in
unison).
Standing waves cannot exist unless they divide their
medium into an integral number of half waves with their nodes. A
standing wave having a fractional
wavelength cannot be sustained.
The same standing waves pattern
can be formed in a three-dimensional box. This pattern will look just
like a highly enlarged crystal, if we assume that the aggregated
particles or grains in the box fluid are analogous to the atoms in a
crystal.
The
key word in standing waves is order.
In short, by using sound we have introduced order where previously
there was none.
Any vibrating body that is set in a
standing, resonant motion, produces harmonics. For musical sounds the
harmonic series is usually expressed as an arithmetical proportion:
1,1:2, 1:3, 1:4, 1:5, 1:6...1:n.
The first and second harmonics
are separated by an octave, frequency ratio 2:1, the 2nd and 3rd by a
perfect fifth (3:2), the 3rd and 4th by a perfect fourth (4:3), and
4th and 5th by a major third (5:4), and the 5th and the 6th by a
minor third (6:5), and so on.
A
composed (periodic) tone contains a multiple of various frequencies
in whole numbers, (integers – 2,3,4,5,6…25…) of
the fundamental frequency.
They are named harmonics. Each
voice or musical instrument produces its own characteristic set of
harmonics, also called formats, that enable the ear to identify the
sound because the ear and the brain perform a Fourier analysis of the
sound. (Some wind instruments, for example, produce only odd
harmonics).
In order to understand the composed
tone, one has to turn to a French mathematician from the 19th
Century, Jean-Baptiste Fourier, who in 1822 proved that any complex
periodic curve – in this case any tone – is composed of a
set of sine curves that contain the
fundamental sine frequency + another sine curve with double the
frequency + a sine curve with triple the frequency, and so on.
A simple Harmonic
motionis typified by the motion of a pendulum,
which is sinusoidal in time and demonstrates a single resonant
frequency.
The formula for The Harmonic Series is the sum, ∑
1/n = 1 + 1/2 + 1/3 + 1/4 + 1/5 +1/6
+…diverges to infinity, when n goes from 1 to infinity.
Another common way to express the harmonics is, the fundamental f,
then 2f, 3f, 4f, 5f....nf harmonic.
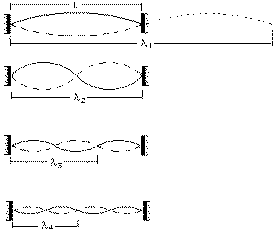
To have an idear of the harmonics
in the string you have to imagine
an idealized stretched string with fixed ends vibrating the first 4
modes of the standing waves. This can be expressed as the
relationship between wavelength, speed and frequency, a basic formula
where the wavelength is inversely proportional to the frequency when
speed is a constant (k) since it is the same string:
Let's work out the
relationships among the frequencies of these modes. For a wave, the
frequency is the ratio of the speed of the wave to the length of the
wave: f = k/wavelength. Compared to the string length L, you can see
that these waves have lengths 2L, L, 2L/3, L/2. We could write this
as 2L/n, where n is the number of the harmonic.
The fundamental or first
mode has frequency f1 = k/wavelength = k/2L,
The second
harmonic has frequency f2 = k/wavelength = 2k/2L = 2f1
The
third harmonic has frequency f3 = k/wavelength = 3k/2L =
3f1,
The fourth harmonic has frequency f4 =
v/wavelength = 4k/2L = 4f1, and, to generalize, The nth
harmonic has frequency fn = k/wavelength = nk/2L = nf1.
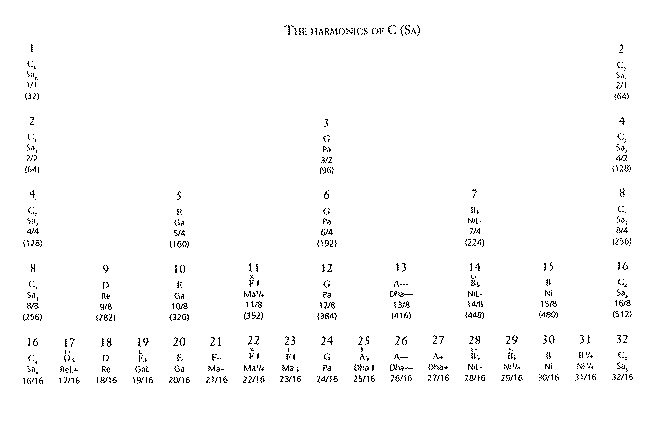 All
waves in a string travel with the same speed, so these waves with
different wavelengths have different frequencies as shown. The mode
with the lowest frequency (f1) is called the fundamental.
All
waves in a string travel with the same speed, so these waves with
different wavelengths have different frequencies as shown. The mode
with the lowest frequency (f1) is called the fundamental.
Note that the n'th mode
has frequency n times that of the fundamental. All of the modes (and
the sounds they produce) are called the harmonics of the string. The
frequencies f, 2f, 3f, 4f etc are called the harmonic series.
The diagram displays the
harmonics in a span of 5 octaves, where the fundamental is C with the
frequency of 32 Hz. As the octaves progress the numberes of new
harmonics increase with the factor of 2.
How Nature performed such a
mathematical division, an arithmetic progression, is beyond my
apprehension, but it is surely a mighty prominent and well-proven
law. Intuitively I feel that the number 2, or its inversion ½,
is the mega number. Remember the integer numbers of ½ waves
(nodes) in the standing wave.
The harmonic series is special
because any combination of its vibrations produces a periodic or
repeated vibration at the fundamental frequency.
The
Harmonic Scale
Since the harmonic series plays such an
important part in music, it should be obvious to use the harmonic
series as the notes in a scale. This is also valid since the harmonic
series contains all the possible intervals used in music, although
the order in which those intervals appear does not properly
constitute a musical scale. The main difficulty is that all its
intervals differ from one another and become smaller as the scale
rises.
The problem with modulation is obvious
since each interval is not alike. Further, the need for a fixed
structure to establish a musical scale, a body of harmony established
by the three prime intervals, cannot be fulfilled by using the
harmonic series as a musical scale.
Nevertheless, the series of
the first sixteen harmonics can be considered to form a mode that is
interesting in comparison with the musical scales used throughout the
history of music.
If we take C as a starting point, we
first notice the appearance of the octave, C', 2/1, then the fifth,
G, 3/2, then the third, E, 5/4, then the harmonic Bb 7/4 –
lower than the usual Bb, and forming with upper C', the maximum tone
8/7.
After this appears the major second, D, 9/8, which forms
with E a minor second, 10/9.
Then come the harmonics F#, 11/8, A-,
13/8, and finally, the seventh, B, 15/8.
The remaining eight
of the first sixteen harmonics add no new notes, as they are at exact
octave intervals from earlier harmonics in the series.
We have to
understand the way the harmonic series display itself in a chain of
octaves, where each new octave contains twice as many harmonics as
the last octave.
By looking at the ratios, the
denominator indicates the octave, the numerator states the number of
harmonics in that octave. Considering only the first sixteen
harmonics, we thus obtain a scale of eight tones formed of the
following intervals:
|
Notes
|
C
|
D
|
E
|
F#
|
G
|
A-
|
Bb
|
B
|
C'
|
|
Ratios
|
1/1
|
9/8
|
5/4
|
11/8
|
3/2
|
13/8
|
7/4
|
15/8
|
2/1
|
|
Savarts
|
|
51
|
46
|
41
|
38
|
35
|
32
|
30
|
28
|
Notice that each
interval gets smaller as the pitch rises.
Calculations
of sound ratios
Another feature in the realm of sound is
the exponential factor, because sound, like many other physical
events, behaves exponentially - not in straight lines. Harmonics
are not linear either.
There are two ways to calculate ratios
of frequencies:
1) One can work with the ratios as they are,
often pretty long numbers, and the calculation is a bit twisted,
since in adding two sound ratios one has to multiply; to subtract you
have to divide; and to divide a sound ratio you have to take the
square root.
A common example is the Equal Temperament, where the
octave has to be divided into 12 equal parts.
One semitone is the
12th root of 2, (21/12) . If you want to divide the whole
tone, 9/8, you have to take the square root of 9/8, or (9/8)½
= 3/2*2½.
2) The other way, which makes the
calculation more straightforward, is to convert
the ratios into logarithmic unities such as cents or savarts.
Logarithmic calculations make it easier to operate with pitch
intervals or frequency ratios, since the size of a pitch interval is
proportional not to the frequency ratio, but to the logarithm of the
frequency ratio. This makes the calculation of ratios simpler,
by a plain process of adding, subtracting or dividing.
Savarts, named after a
French physicist, and cents are both logarithmic
systems developed to make it easy to compare intervals on a linear
scale instead of using fractals or frequency ratios (f2/f1).
A
Savart is calculated as the logarithm (base 10) of the frequency
ratio and, for convenience, multiplied by 1000. We then have an
interval expressed in terms of a savart unit.
The interval
of an octave in savarts is the logarithm of 2, which is 0.3010...
expressed as 301 savarts.
Savarts have an advantage over the
widely used American system, cents, since savarts is designed to fit
any frequencies ratios (f2/f1), while cent by definition is based on
one scale, the 12 semitones in the Equal Temperament.
Cent is also a logarithmic
unit, which by definition is based on the tempered scale of 1200
cents/octave. A semitone is therefore 100 cents. This definition is a
bit more complicated than the plain savart, since the exact
relationship of frequencies to cents is expressed by this formula:
1200 * (f2/f1) / log 2 = 3986 * log10
(f2/f1).
E.g. the interval of the perfect fifth calculated in
cents is: the log10 3/2 = 0.1761.. The fifth in cents is
3986 * 0.1761 = 702 cent.
The
Octave
This interval is the very most
outstanding division of sound and music and is recognized in all
musical traditions through time on the globe. The division of the
octave has been made differently depending on musical tradition, but
alr the world in all times the octave has been recognized as the
basic unit that constitutes a beginning and an end.
‘Octave’
derives from Latin and means the ‘eighth’. It is the 8th
step in the diatonic scale consisting of 7 tones, 5 full tones and 2
semitones. The eighth tone in the diatonic scale, which is the most
common in the world, completes the octave on a pitch that in
frequency is the double of the fundamental tone.
Graphically, one could say that an
octave expresses or represents a circle. Several octaves shape a
spiral, where the same fundamental is above or below. The obvious
mystery about octaves is that tones an octave apart sound similar,
though the frequency is the double or the half.
They pertain, so
to speak, to the same family; from the same root, unfolding in the
spectrum of frequencies. They have the same Chroma.
They always double up the frequencies in the ascending mode or halve
them in the descending mode.
Again we see the basic, universal
division of one into two, as we first mentioned in the paragraph
about the standing waves. Just remember the awesome sight of the
pregnant egg-cell dividing itself. The law of octaves belongs not
only to the realm of sound, but can be observed as manifesting itself
throughout Nature around, and in astronomy above.
The Fourth
The very harmonious Fourth is a kind of
a puzzle, with its prime interval in the ratio of 4 : 3. It is not
represented in the first 16 harmonics in the series, though the 3rd
and 4th harmonics are separated by a Fourth. It has taken me some
time to figure it out.
In order to understand the importance of
the Fourth, we have to look at the previous prime interval, the
Fifth, with the ratio of 3 : 2. The 2nd and 3rd harmonics are
separated by a Fifth. These two intervals together constitute an
octave. They are complementary intervals.
Furthermore, by going down by a Fourth
into the octave below, one reaches the Fifth in the sub-octave, which
has half the frequency. In other words: a descending Fifth, 2:3,
divided by ½, equals 4:3, a Fourth.
In the musical language the Fifth is
called the Dominant and the Fourth the Sub-dominant, which plays a
very dominant role in music all over the world.
In all the
musical scales that are obtained by the generating interval 3:2, the
opposite movement – lowering by 4:3 – makes it possible
to fit the generated intervals into one octave.
Music
and mathematics
Music
and Numbers are often said to be as brother and sister,
different but related. In addition, we have to take into
consideration numerical representation, which plays an important role
in Eastern music but is ignored in the Western tradition.
Composite
sound
A musical sound or tone is a composite
sound containing a multiple of overtones or harmonics. In musical
practice the tone is not only dependent on its pitch and amplitude
(loudness), but also on its specific numbers of harmonics (formats),
which ‘color’ the tones so that each instrument or voice
has its characteristic sound.
This has nothing to do with
musical compositions aiming to ‘paint’ colors, or the
blue notes in jazz music. ‘Overtone’ originates from the
German Obertone, which refers to the various numbers of partials or
harmonics that are produced by the strongest and lowest fundamental
note, and fused into a compound or complex tone.
In his book On the Sensation of Tone
from 1877, Herman von Helmholtz formulated the theory about the
consonant and dissonant intervals based on the numbers of beats
generated when two tones or a chord are played.
It was first
about 100 years later that Promp was able to prove a more consistent
theory, the Consonant Theory, which now is generally accepted.
Beats
When two tones (or chords) are played
simultaneously, another important acoustic phenomenon takes place,
called ‘beats’. When the frequencies of two tones are
close to each other, a periodical beat can clearly be heard, caused
by the interference of the different waves, which alter the amplitude
so an intensified rhythmic beating, floating tone is heard as a third
tone.
There are other interference patterns besides beat
frequencies, but this will do in this instance.
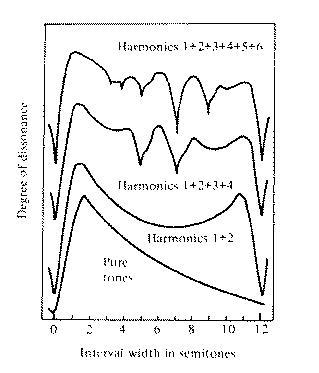 Some
intervals or chords produce more beats in the higher harmonics than
others, and those are picked up by the ear as unclean, muddy or
unpleasant, and are labeled dissonant.
Some
intervals or chords produce more beats in the higher harmonics than
others, and those are picked up by the ear as unclean, muddy or
unpleasant, and are labeled dissonant.
The intervals which make fewest beats
are called consonant, such as an octave, the perfect fifth, the
perfect fourth – the three prime intervals, or ‘The body
of Harmony’ as described by Aristotle; the basis for the
musical scale.
A general rule about sound ratios is
that the simpler the ratios between sounds are, the more their
relations are harmonious, while the more complicated the ratios are,
the more dissonant are the sounds.
Pythagoras was the first in the West to
formulate the law of musical pitches depending on numerical
proportions. From this he based his underlying principle of
‘harmonia’ as a numerical system bound together by
interlocking ratios of small numbers. This discovery probably led him
to the idea of the Harmony of the Spheres.
His vision of ‘The
Music of the Spheres‘ aroused deep emotions in me. It
alludes to the seven planets known at that time, and has puzzled
generations since it was declared. Johannes Kepler dedicated most of
his life to attempting to solve that notion.
The
auditory system
The receiving part, the human ear, is
equally important. The recent discoveries (The Consonant Theory) of
the function of the basal membrane in Cochlea as a Fourier analyzer,
and the role the critical band plays in the perception of rough or
smooth sound, dissonance and consonance, gives a consistent theory
for some of the hearing functions.
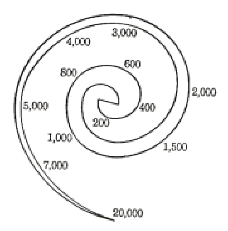 When
the frequency ratios are narrowed down to such small intervals that
our auditory system is not capable of differentiating, the harmonics
become fused because of the critical band, a relatively new
discovery, (around 1970-80 by Plomp a.o.) which refers to the
overlapping amplitude envelopes on the basilar membrane in the Organ
of Corti in the Cochlea.
When
the frequency ratios are narrowed down to such small intervals that
our auditory system is not capable of differentiating, the harmonics
become fused because of the critical band, a relatively new
discovery, (around 1970-80 by Plomp a.o.) which refers to the
overlapping amplitude envelopes on the basilar membrane in the Organ
of Corti in the Cochlea.
Trained ears are able to detect the
harmonics up to the 6th or 7th harmonics.
←Schematic
graph
of the Cochlea
When the interval between two tones
decreases, their amplitude envelopes overlap to an increasing extent.
A rough, harsh tone will be heard, which anyone can hear when two
notes with less than minor 3rd separation
are played simultaneously. This is very shortly the key to understand
the theory of dissonance and consonants, which is the foundation in
the origin of scales.
There are a lot of more acoustic laws
and theories of fusion of pure tone components and other acoustic
phenomena such as masking, except to state that the inner ear
performs a partial frequency analysis of
a complex musical tone, a Fourier analysis, sending to the brain a
distinct signal recording the presence of each of the first seven or
eight harmonic components; in addition the brain receives signals
from the part of the basilar membrane activated by the unresolved
upper harmonics.
Several experiments by different
scientists suggest that the brain determines the pitch of a complex
tone by searching for a harmonic pattern among the components
separately resolved in the inner ear. If the deviation from a true
harmonic series is too large, the brain gives up the attempt to find
a single matching set of harmonics. Then the components are heard
separately, rather than as a fused tone.
This
explains the ‘missing fundamentals’ in the harmonic
spectrum of a bassoon playing E3, because the ear does not ‘hear’
the fundamental tone, but the harmonic.
Breakthrough
in the science of hearing
Helmholtz beat theories was commonly
accepted for about 100 years, before the Noble Prize winning
Hungarian scientist Békésy in 1960 made a new
breakthrough by his discovery of the role the basilar membrane plays
in the hearing of pitch.
He
derived by anatomical studies a relationship between distance along
the basilar membrane and frequency of maximum response. A high
frequency pure tone generates a wave that travels only a short
distance along the basilar membrane before reaching its peak
amplitude; the hair cells at the position of the peak are fired, and
the brain receives signals from the corresponding nerve fibers. These
fibers evoke a ‘high frequency’ sensation.
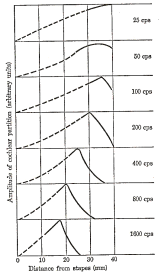 A
low frequency tone generates a wave that travels most of the way to
the helicotrema before rising to its peak amplitude and dying away.
Signals from nerve fibers connected to this region of the basilar
membrane evoke a ‘low-frequency’ sensation in the brain.
A
low frequency tone generates a wave that travels most of the way to
the helicotrema before rising to its peak amplitude and dying away.
Signals from nerve fibers connected to this region of the basilar
membrane evoke a ‘low-frequency’ sensation in the brain.
Other theories than the above ‘place
theory’ have been brought forward, among them the ‘temporal
theories’, i.e. emphasizing the use of the timing information
in nerve signals.
Helmholtz
dismissed
The modern Consonance Theory of Plomp
extended the discoveries of Békésy with some new
important findings, that gave whole new meanings to the concept of
hearing. The beat theory of Helmholtz was finally dismissed
in favor of the well experimented and proven Consonance Theory, in
which the ears Discrimination Frequency and its Critical Bandwidth
plays an important part.
The
Critical Band
As the interval between two tones
decreases, their amplitude envelopes on the basilar membrane overlap
to an increasing extent. A significant number of hair cells will now
be responding to both signals. When the separation is reduced, e.g.
to a tone, the amplitude envelopes overlap almost completely,
implying a strong interaction between the two sounds, which is heard
as a harsh, rough sound: a dissonance.
When
two pure tones are so close in frequency that there is a large
overlap in their amplitude envelopes, we say that their frequencies
lie within one critical
band.
This concept has been of great importance in the development of
modern theories of hearing and, one must add, gives a much better
explanation for the ear’s determination of consonant or
dissonant intervals.
Logarithmic
intervals and frequency distributions
This portion is a bit of off the key
with the musical scales. However, when (in 2007) I read about
Cislenko's logarithmic intervals in the book Tools of Awareness, I
felt immediately that here is new, first-class research about the
basic concept of a scale. You have to go above the level of sound and
reach up to the level of sizes of bodies.
In 1980, the Russian biologist Cislenko
published what is probably one of the most important biological
discoveries of the 20th century. The published work was Structure of
Fauna and Flora with Regard to Body Size of Organisms
(Lomonosov-University, Moscow).
His work documents that segments
of increased species representation were repeated on the logarithmic
line of body sizes in equal intervals (approx 0.5 units of the
decadal logarithm).
The phenomenon is not explicable from a
biological point of view. Why should mature individuals of
amphibians, reptile, fish, bird and mammals of different species find
it similarly advantageous to have a body size in the range of 8 - 12
cm, 33 - 55 cm or 1,5 - 2,4 m?
Cislenko assumed that competition in the
plant and animal kingdoms occurs not only for food, water or other
resources, but also for the best body sizes.
Each species tries to occupy the advantageous intervals on the
logarithmic scale where mutual pressure of competition also gave rise
to crash zones.
However, Cislenko, was not able to explain, why
both the crash zones and the overpopulated intervals on the
logarithmic line are always of the same length and occur in equal
distance from each other. He was unable to figure out why only
certain sizes would be advantageous for the survival of a species,
and what these advantages actually were.
The
logarithmic frequency distributions by Dr. Hartmut Mulier
Cislenko's work inspired the German
scientist Dr. Hartmut Müller to search for other scale-invariant
distributions in physics. The phenomenon of scaling is well known to
high-energy physics.
Müller found similar frequency
distributions along the logarithmic line of sizes, orbits, masses,
and revolution periods of planets, moons and asteroids. Being a
mathematician and physicist he did not fail to recognize the cause
for this phenomenon in the existence of a standing pressure wave in
the logarithmic space of the scales/measures.
Scale is what physics can measure. The
result of a physical measurement is always a number with measuring
unit – a physical quantity.
Imagine
that we have measured 12cm, 33cm and 90cm. Choosing 1 cm as the
standard measure (etalon), we will get the number sequence 12 - 33 -
90 (without measurement unit, or as the physicist says: with unit 1).
The distances between these numbers on the number line are 33 - 12 =
21 and 90 - 33 = 57.
If
we were to choose another measuring unit, such as the etalon with
49,5cm, the number sequence would be 0,24 - 0,67 - 1,82. The
distances between the numbers have changed into 0,67 - 0,24 = 0,42
and 1,82 - 0,667 = 1,16.
However, on the logarithmic line, the
distance will not change, no matter what
measuring unit we choose. It will always remain constant.
In
our example, this distance amounts to one unit of the natural
logarithm (with radix e = 2,71828...): ln 33 - ln 12 ≈ ln 90 -
ln 33 ≈ ln 0,67 - ln 0,24 ≈ ln 1,82 - ln 0,67 ≈ 1.
Physical values of measurement, therefore, own the remarkable feature
of logarithmic invariance (scaling).
So,
in reality, any scale is a logarithm!
Any scale
is a logarithm
It is very interesting that natural
systems are not evenly distributed along the logarithmic line of the
scales. There are ‘attractive’ sections which are
occupied by a great number of completely different natural systems;
and there are ‘repulsive’ sections that most natural
systems will avoid.
Growing crystals, organisms or
populations that reach the limits of such sections on the logarithmic
line will either grow no more or will begin to disintegrate, or else
will accelerate growth so as to overcome these sections as quickly as
possible.
The Institute for
Space-Energy-Research I.M. was able to prove the same phenomenon also
in demographics (stochastic of world-wide urban populations), economy
(stochastic of national product, imports and exports world-wide) and
business economy (stochastic of sales volume of large industrial and
middle-class enterprises, stochastic of world-wide stock exchange
values).
The borders of ‘attractive’
and ‘repulsive’ segments on the logarithmic line of
scales are easy to find because they recur regularly with a distance
of 3 natural logarithmic units. This distance also defines the
wavelength of the standing pressure wave: it is 6 units of the
natural logarithm.
In fact, the world of scales is
nothing else but the logarithmic line of numbers known to mathematics
at least since the time of Napier (1600). What is new, however, is
the fundamental recognition that the number line has a harmonic
structure, which is itself the cause for the standing pressure
wave.
Leonard Euler (1748 )
had already shown, that irrational and transcendental numbers can be
uniquely represented as continued fractions in which all elements
(numerators and denominators) will be natural numbers.
Prime
numbers
In 1928, Khintchine succeeded in
providing the general proof about prime numbers. In the theory of
numbers this means that all numbers can be constructed from natural
numbers; the universal principle of construction being the continued
fraction. All natural numbers 1, 2, 3, 4, 5, ... in turn are
constructed from prime numbers, these being natural numbers which
cannot be further divided without remainder, such as 1, 2, 3, 5, 7,
11, 13, 19, 23, 29, 31, ... (traditionally 1 is not classed as a
prime number although it fulfills all criteria).
The distribution of prime numbers on the
number line is so irregular that so far no formula has been found
that would perfectly describe their distribution.
Dr. Muller found
that the distribution of numbers is indeed very irregular - but only
on the linear number line.
On the logarithmic number line, large
gaps of prime numbers recur at regular intervals. Gauss (1795) had
already noticed this.
The reason for this phenomenon is the
existence of a standing density wave on the logarithmic number line.
The node points of this density wave are acting as number attractors.
This is where prime numbers will 'accumulate' and form composite
numbers, i.e. non-primes, such as the 7 non-primes from 401 to
409.
Hence a ‘prime number gap’ will occur in this
place. Precisely where non-primes (i.e. prime clusters) arise on the
logarithmic number line, there it is that matter concentrates on the
logarithmic line of measures. This is not magic; it is simply a
consequence of the fact that scales are logarithms, i.e. ‘just’
numbers.
So the logarithmic line of scales is
nothing else but the logarithmic number line. And because the
standing pressure wave is a property of the logarithmic number line,
it determines the frequency of distribution of matter on all
physically calibrated logarithmic lines - the line of ratios of size,
that of masses, of frequencies, of temperatures, velocities,
etc.
Finding a node point on the logarithmic line is relatively
easy, since the wavelength of the standing density wave on the
logarithmic number line is known, and the calculation of all nodal
points is done by a simple formula.
The distance between adjacent
node points is 3 units of the natural logarithm.
The frequency ranges around 5 Hz, 101
Hz, 2032 Hz, 40,8 kHz, 820 kHz, 16,5 MHz, 330,6 MHz, etc. are
predestined for energy transmission in finite media. This is also
where the carrier frequencies for information transmission in
logarithmic space are located.
Frequencies that occur near a note
point are very common in nature, as well as in technological
applications.
I
wish to thank Dr. Willy de Maeyer for his help in the subject of this
deeper scientific nature of scales. More similar kinds of
mind-puzzling statements in sound and music can be found on my page
The Sound of Silence.
This is a brief resume of those factors
in hearing that are closely related to perceiving an interval or
chord. We will skip the many other acoustic phenomena, because here
we will only try to give an account of the reasons why musical scales
are created as they are.
Thomas Váczy Hightower, ©
2002. (edited 2009)
To
continue in part II of The Creation of Musical Scales,
Index
Your comments: mailto: mail@vaczy.dk
 To
produce sounds, a vibrating body, an oscillator,
is needed.
To
produce sounds, a vibrating body, an oscillator,
is needed. 
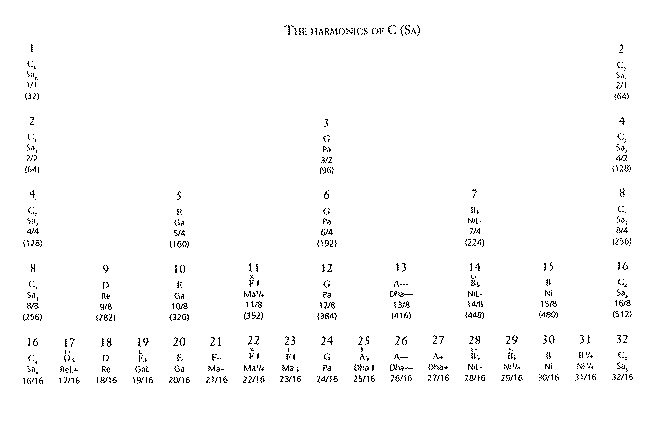
 When
the frequency ratios are narrowed down to such small intervals that
our auditory system is not capable of differentiating, the harmonics
become fused because of the critical band, a relatively new
discovery, (around 1970-80 by Plomp a.o.) which refers to the
overlapping amplitude envelopes on the basilar membrane in the Organ
of Corti in the Cochlea.
When
the frequency ratios are narrowed down to such small intervals that
our auditory system is not capable of differentiating, the harmonics
become fused because of the critical band, a relatively new
discovery, (around 1970-80 by Plomp a.o.) which refers to the
overlapping amplitude envelopes on the basilar membrane in the Organ
of Corti in the Cochlea. 