How to calculate oscillation of a body into freqency:
The
length of
time a celestial body requires to rotate around its axis and to revolve
around the sun, can be converted into sound (and
color) by means of the law of the octave.
Any things that moves or oscillate has a
frequency measured in a time unit, usually one second and is called Hertz after
the German physicist. Frequency express the number of
repetitions of a periodic phenomenon during a
certain length of time. (A tuning fork that vibrates 272 times back and forth in
one second, has a frequency at 272 Hertz (Hz.)).
Time
is not a concept of its own, but a duration. Oscillation is a repetition of the
same phenomenon,
e.g. the movement of a string, the swing of a pendulum, or astronomical
constellations such as a day or a year.
There
is a simple relationship between the period of oscillation
(the time it takes to move back and forth) and its frequency. It is an inverse
proportion: the
Frequency range can be
measured in a basic unit called octaves. In practice one can
form an octave by multiply or divide the frequency with 2.
This interval is the very most outstanding division of sound and music and is recognized in all musical traditions through time on the globe. The division of the octave has been done differently depending of musical tradition, but all over the world in all times the octave has been recognized as the basic unit that constitute a beginning and an end.
Octave derived from Latin and means the eighth.
It is the 8th step in the diatonic scale consisting of 7 tones, 5
full tones and 2 semi tones. The eighth tone in the diatonic scale, which is the
most common in the world, complete the octave on a pitch, that in frequency is
the double of the fundamental tone.
Graphically
one could say that an octave express or represent a circle. Several octaves
shapes a spiral where the same fundamental is above or below. The straight out
mysterious about octaves is that tones an octave apart sounds similar though the
frequency is the double or the half. They contain so to speak to the same family; from the same root, unfolding in the spectrum of frequencies.
They have the same Chroma.
The
whole time double up the frequencies in the ascending mode or halve in
descending mode.
Again
we see the basic, universal division of one into two as we first refer to in the
paragraph about the standing waves.
Just
remember the awesome sight of the pregnant egg-cell dividing itself.
The
law of octaves belong not only to the realm of sound but can be observed as
manifesting itself though out Nature and above in astronomy.
Two tones an octave apart are
perceived as having a kindred relationship - as being, in a sense, "the
same note". This recognition of similarities for tones an octave apart is
and was applying to any major musical culture all over the globe since the
beginning of the history of man.
The sense of pitch associated with a
tone has two different attributes: the frequency of the tone, the ”height”,
and the chroma, which is a quality shared by all notes described by a particular
letter. (Bachem 1950) Thus C2 and C3 are separated in
pitch by an octave, they both have the same chroma
- that associated with all C’s. They are in the same family.
In one interpretation of the pattern
recognition theory of pitch, the brain searches for a distribution of peaks
along the basilar membrane corresponding to a harmonic series of vibrations. On
this basis, the fact that C2 and C3 evoke almost the same
sensation can be readily understood.
The sound wave is a chain reaction where the
molecules of air by elastic beats push the other molecules in the longitudinal
direction quiet similar to a long train getting a push from a locomotive.
The
sound waves shall not be mistaken as waves
in water caused by e.g. a stone in a pond, though the picture appears to be
alike.
Sound waves are longitudinal,
back and forth.
Another feature in the realm of sound is the exponential factor, because
sound as many other physical events behaves exponentially - not in straight
lines.
There are two ways to calculate ratios of frequencies:
1) One can work with the ratios
as they are, and when adding two sound ratios one have to multiply; to subtract you have to divide, and to divide a sound ratio you have to
take the square root.
A common example: in order to divide the octave into 12 equal parts as the case
is for the Equal Temperament. You have to calculate the 12th. root of 2, (21/12)
. If you want to divide the whole tone, 9/8, you have to take the square
root of 9/8, or (9/8)½ = 3/2*2½ .
2) The other way, which makes the calculation
more straight forward, is to convert the
ratios into logarithmic unities such as cent or savarts,
which makes the calculation of ratios more simple by adding, subtraction and dividing.
Savarts named after a French physicist and cents are logarithmic systems
developed to make it easy to compare intervals on a linear scale instead of using
fractals or frequencies ratios.
Savarts is calculated as the logarithm
(base 10) of the frequency ratio and, for convenience, multiply with 1000. We
shall then have an interval expressed in terms of a unit call savarts.
The
logarithm of 2 being 0.3010... the interval of the octave is equal to 301 savarts.
Savarts is more exact than the widely used American system,
cents, which by definition is based on the tempered scale of
1200 cents.
Cent is also a logarithmic unit,
which make it easier to operate with pitch intervals or frequencies ratios,
since the size of a pitch interval is proportional not to the frequency ratio, but to the
logarithm of the frequency ratio.
It is a simple relationship: pitch interval
(in octaves) = log2 (f2 : f1). Since there are
chosen to have 1200 cents in an octave, this is equivalent to:
pitch interval
(in cents) = 1200 * log2 (f2 : f). In practice, logarithms
to base 10 (log10) are normally used.
Plucked
strings exhibit transverse waves in a back and forth movements locally
producing a pulse along the direction in which the
wave itself travels with a speed depending of the mass of the string and its
material but usually lower than airwaves. A good explanation is given by The
University of New South Wales, Australia.
(The frequency of the string itself is the same
as the frequency of the air waves.
The wavelength is different due
to the dissimilarity in speed.)
The lengths of the vibrating part of the string is inverse proportional to the frequencies. The period of oscillation = 1 / frequency. This is a important acoustic law, that applies to any conversion of period into frequencies. If you, e.g. divide an octave string with 2/3, the ratio of the sound will be 3/2 of an octave, a fifth.
To produce sounds a vibrating body, an
oscillator, is needed.
The
heart and aorta formed a special resonant system when breathing is ceased. Then
the heart beat seems to wait until the echo returns from the bifurcation (where the
aorta forks out in the lower abdomen). Then the next heart beat sets in. In this
synchronous way a resonant, standing wave of blood is established with a
frequency about seven times a second. This harmonious mode requires for its
sustenance a minimum amount of energy, which is an intelligent response from the
body. In deep meditation a similar mode is established. It is interesting to notice
that this mode of 7 Hz is closed to the Schumann resonance.
Standing
waves are a kind of echo, that moves back and forth, since the waves are
reflected between two solid points, basically, a hamper or fixed string. For
wind instruments with an open end, the impedance (the resisters from the air)
works in a similar manner. There are also closed pipes, that resonates a bit
different.
When
a fixed string is plucked, the potential energy is released in a transverse wave,
that in a split second begins to displace a division
of the string in different moving parts, where some points are not moving, which
are called nodes.
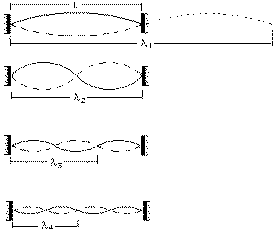
How many nodes the string is
divided into when it vibrates depends of the material, the tension, and
especially how and where it is plucked or bowed ,etc, but here we try to get a
general picture of the nature of standing waves in a plucked string.
When
the potential energy is stopped in the fixed ends,
the kinetic energy is at its maximum and continue in a 180°
phase shift the opposite way. We have two waves with the same frequency and
amplitude traveling in the opposite direction. Where the two waves add together
or superpose, movements is cancel out and we have moving less nodes. That occur a half wavelength apart and
constitute the standing waves.
The
repeating shifts between potential and kinetic energy in a moving string draws
ones attention to a similar pattern we can observe in a pendulum and its simple
harmonic motion.
The
numbers of nodes, the no moving points, in a standing wave, is equal to the
number of harmonics or partials created in
the standing wave.
The
same pattern can be observed with fine sand on a metal plate in vibration by a
bow. The standing waves automatically divide the length and width of the plate
into an integral number of half wave-lengths. It
is only then, a standing wave can be sustained. That pattern is the most energy effective
form nature can provide. (A similar pattern is the rhythm entrainment, where
random oscillation after a while begin to oscillate in unison).
Standing
waves can not exist unless they divide their medium into an integral numbers of
half waves with its nodes. A standing waves having a fractional wavelength can
not be sustained.
Any
vibrating body that is set in a standing, resonant motion,
produce harmonics. For musical sounds the harmonics series is usually
expressed as a arithmetical proportion:
1,1:2,
1:3, 1:4, 1:5, 1:6...1:n.
The
first and 2nd harmonics are separated by an octave, frequency ratio 2:1, the 2nd
and 3rd by a perfect fifth (3:2), the 3rd and 4th by a perfect fourth (4:3), and
4th and 5th by a major third (5:4), and the 5th and the 6th by a minor third
(6:5), and so on.
A
simple Harmonic motion is typified by the motion of a pendulum
and is sinusoidal in time and demonstrate a
single resonant frequency.
The
formula for The Harmonic Series is the sum,
Since the Harmonic Series is so important in the construction of musical scales, another common way to express the harmonics is a simple multiplication by whole numbers: the fundamental f, then 2f, 3f, 4f, 5f....nf harmonic.
How
Nature performed such a mathematical division, an arithmetic
progression is beyond my apprehension, but it is surely a mighty
prominent and well proofed law. Intuitively I feel that the number 2 or its
inversion ½ is the mega number. Remember the integer numbers of ½ waves
(nodes) in the standing wave.
The harmonic series is special because any combination of its vibrations produces a periodic or repeated vibration at the fundamental frequency.
Imagine an idealized stretched string with fixed ends vibrating the first 4 modes of the standing waves. This can be expressed as the relationship between wavelength, speed and frequency, a basic formula where the wavelength is inversely proportional to the frequency when speed is a constant (k) since it is the same string:
Let's work out the relationships among the
frequencies of these modes. For a wave, the frequency is the ratio of the speed
of the wave to the length of the wave: f = k/wavelength. Compared to the string
length L, you can see that these waves have lengths 2L, L, 2L/3, L/2. We could
write this as 2L/n, where n is the number of the harmonic.
The fundamental or first mode has frequency f1
= k/wavelength = k/2L,
The second harmonic has frequency f2 = k/wavelength = 2k/2L = 2f1
The third harmonic has frequency f3 = k/wavelength = 3k/2L = 3f1,
The fourth harmonic has frequency f4 = v/wavelength = 4k/2L = 4f1,
and, to generalize,
All waves in a string travel with the same speed,
so these waves with different wavelengths have different frequencies as shown.
The mode with the lowest frequency (f1) is called the fundamental. Note that the
nth mode has frequency n times that of the fundamental. All of the modes (and
the sounds they produce) are called the harmonics of the string. The
frequencies f, 2f, 3f, 4f etc are called the harmonic series.
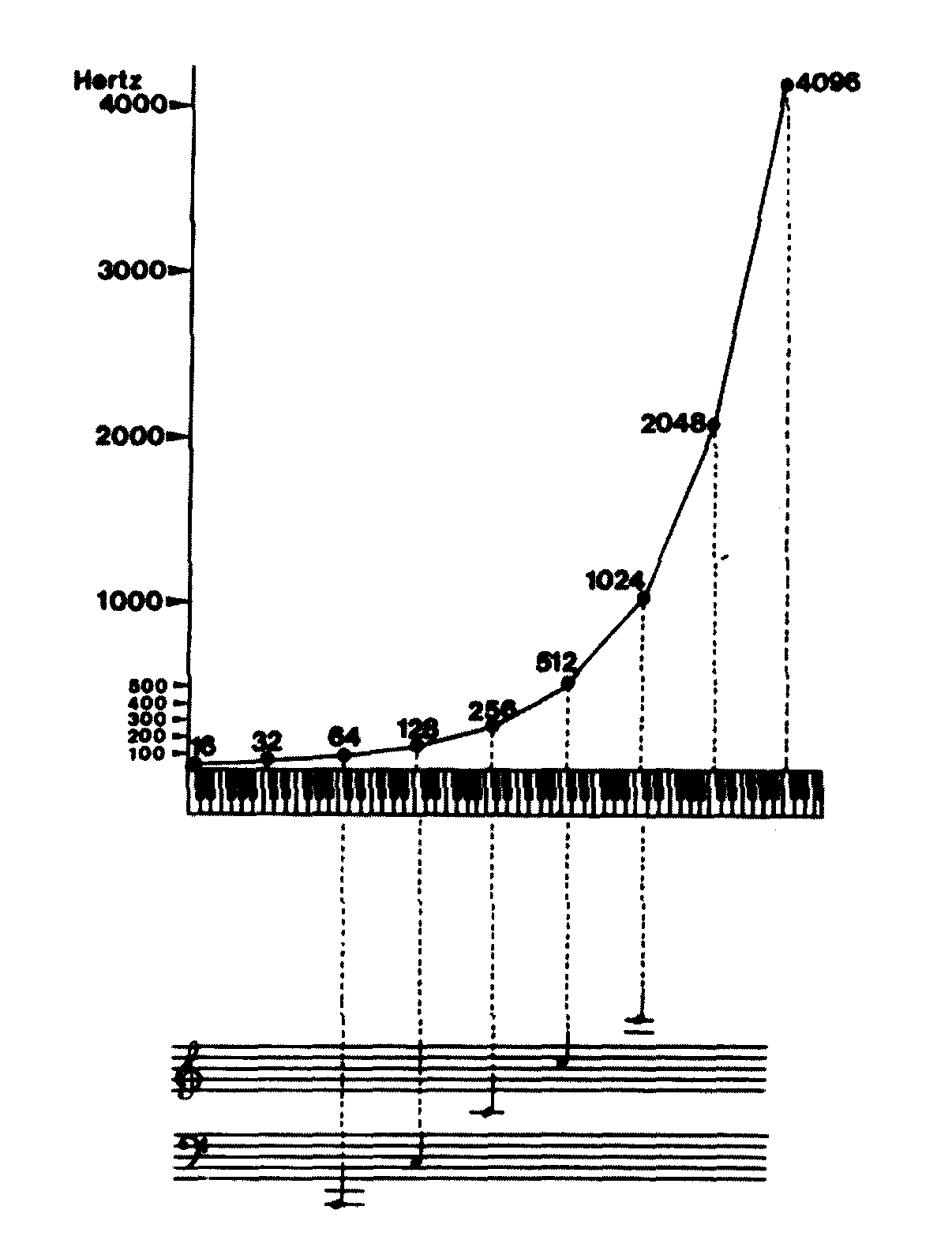
The diagram below displays the harmonics in a span of 5 octaves, where the fundamental is C with the frequency of 32 Hz. As the octaves progress the numberes of new harmonics increase with the factor of 2.
A
musical sound or a tone is a composite sound containing a multiple amount of
overtones or harmonics.
This has nothing to do with musical compositions aiming to "paint"
colors, or the blue notes in jazz music. Overtones
originate from the German Obertone which refer to the various numbers of
partials or harmonics that are produced by the strongest and lowest fundamental
tone and fused into a compound or complex tone.
Herman
von Helmholtz formulated in his book "On the Sensation of Tone"
from 1877, the theory
about the consonant and dissonant intervals based on the numbers of beats there
are generated, when two tones or a chord are played.
It was first about 100 years
later Promp could prove a more consistent theory, the Consonant
Theory, which now is generally accepted
In
order to understand the composed tone one has to turn to a French mathematician
from the 19th. Century,
A composed (periodic) tone contains a number of various
multiple frequencies in whole numbers, integers, (2,3,4,5,6…25…) of the
fundamental frequency.
They are named harmonics. Each voice or musical
instrument (Some wind instruments, e.g. produce only odd harmonics) produces its
own characteristic set of harmonics, also
called formats, that makes the ear able to identify the sound because the ear
and the brain also perform an Fouier analyze of the sound.
When two
tones (or chords) are played simultaneously, another important acoustic
phenomenon is taking place called beats. It can clearly be heard when the
frequency of the two tones are close to each other as a periodical beat caused
by the interference of the different waves, which alter the amplitude so an
intensified rhythmic beating, floating tone is heard as a third tone. There
are other interference patterns than beat frequencies, but this will do in this
contest
Some
intervals or chords produce more beats in the higher harmonics than others and
those are pick up by the ear as unclean, muddy or unpleasant and are labeled dissonant.
The
intervals which make fewest beats are called consonant, such as an octave,
the perfect fifth, the perfect fourth, the three prime intervals,
“The body of Harmony” as described by Aristotle; the basis for the
musical scale.
A general rule about sound ratios is, that the simpler the ratios between sounds are, the more their relations are harmonious, while the more complicated the ratios are, the more dissonant are the sounds.
Pythagoras was the first in the West who formulated the law of musical pitches
depending on numerical proportions. From this he based his underlying principle of
"harmonia" as a numerical system bound together by interlocking ratios
of small numbers. This discovery probably led him to the idea of the Harmony of
the Spheres.
His vision of "The Music of the Spheres" aroused deep emotions in me. It
alludes to the seven planets known of that time, and has
puzzled generations since it was declared. Johannes Kepler dedicated most of his
life in order to solve that notion.
Helmholtz
beat theories was commonly accepted for about
100 years, before the Noble Prize winning Hungarian scientist Békésy in 1960 made a new breakthrough by his discovery of the role the basilar membrane plays
in the hearing of pitch.
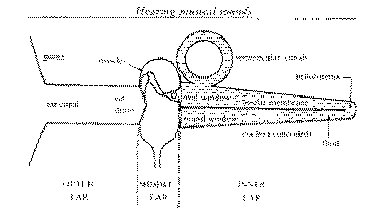
He derived by anatomical studies a relationship between distance
along the basilar membrane and frequency of maximum response. A high frequency
pure tone generates a wave that travels only a short distance along the basilar
membrane before reaching its peak amplitude; the hair cells at the position of
the peak are fired, and the brain receives signals from the corresponding nerve
fibers. These fibers evoke a "high frequency" sensation.
A low
frequency tone generates a wave that travels most of the way to the helicotrema
before rising to its peak amplitude and dying away. Signals from nerve fibers
connected to this region of the basilar membrane evoke a
"low-frequency" sensation in the brain.
Other
theories than the above "place theory" have been brought forward,
among them the "temporal theories", i.e. emphasizing the use of the
timing information in nerve signals.
The
modern Consonance Theory of Plomp extended the
discoveries of Békésy with some new important findings, that gave whole new
meanings to the concept of hearing. The beat theory of Helmholtz was finally
dismissed in favor of the well experimented and proven Consonance Theory, in
which the ears Discrimination Frequency and its Critical Bandwidth plays an
important part.
As the
interval between two tones decreases, their amplitude envelopes on the basilar
membrane overlap to an increasing extent. A significant number of hair cells
will now be responding to both signals. When the
separation is reduced, e.g. to a tone, the amplitude envelopes overlap almost
completely, implying a strong interaction between the two sounds, which is heard
as a harsh, rough sound: a dissonance.
When
two pure tones are so close in frequency that there is a large overlap in their
amplitude envelopes, we say that their frequencies lie within one
critical
band. This concept has been of great importance in the development of modern
theories of hearing and one must add gives a much better explanation for the
ears determination of consonant or dissonant intervals.
For
each 'reference' tone (X axis in the diagram), there is a frequency difference
value (called Discrimination Frequency, 'Discrim. Freq.' label in the diagram),
under which the second tone is not distinguished from the reference tone; for example, the semitone difference (the blue
curve in the diagram) in the dodecaphonic system (12 semi tones Equal
Temperament) is, for each reference tone, under the 'Discrimination Frequency'
curve and can therefore not be detected.
In addition,
for each 'reference' tone, there is a second
important frequency difference value, called 'Critical Band'; if the frequency
difference is below 25% of the Critical Band the two tones are judged 'clearly
dissonant'; if it is between 25% and 50% of the Critical Band (the sky blue
curve in the diagram) the two tones are judged 'partially dissonant'; if it is
more than 50% of the Critical Band, they are judged 'consonant'; for example the tone difference (the
violet curve in the diagram) in the dodecaphonic system is 'consonant' for
reference tone frequencies >
about 500 Hz, where as the minor third difference (the yellow curve in the
diagram) in the dodecaphonic system is 'consonant' for reference tone
frequencies > 300 Hz.
(With
permission by Francesco Caratozzolo, Electronic Engineer (Ph.D. in
Bio-Engineering)).
Main page for the acoustic laws behind the musical scales.